Combinational Logic
CS-A1120 Programming 2
Lukas Ahrenberg
Department of Computer Science
Aalto University
(Based on material by Petteri Kaski and Tommi Junttila)
What are the principles by which computers operate?
How to build machines that compute with bits?
Computing
- "Top-down" : Turing machines
- "Bottom-up" : Gates and circuits
After this round, you
- know how basic logic gates and buses form the basis of computing (bottom-up design)
- can identify basic logic gates, and read and draw simple circuit diagrams
- can combine gates and buses to build logic functions
- can use Scala structures to simulate logic functions
Last round
- A bit is used to represent two states (0/1)
- Sequences of bits can be used to represent data (e.g. a number)
- Boolean operations (AND, OR, NOT,…) is used to transform bits & data
Goal for today
A "machine" that adds up numbers
Warming up
- Given the following (silly) function
- (a Boolean can have two values true or false, which we can think of as a bit)
def f(a:Boolean, b:Boolean) = if a == b then true else false
if
def f(a:Boolean, b:Boolean) = a == b
==, !=, et c), but using Boolean operators (&, |, !)
def f(a:Boolean, b:Boolean) = (a & b) | (!a & !b)
Goal for today
A "machine" that adds up numbers
Construction kit for a computer
- Logic gates NOT, AND, OR
- Some 'wire' to connect them with

Gates as Boolean operations
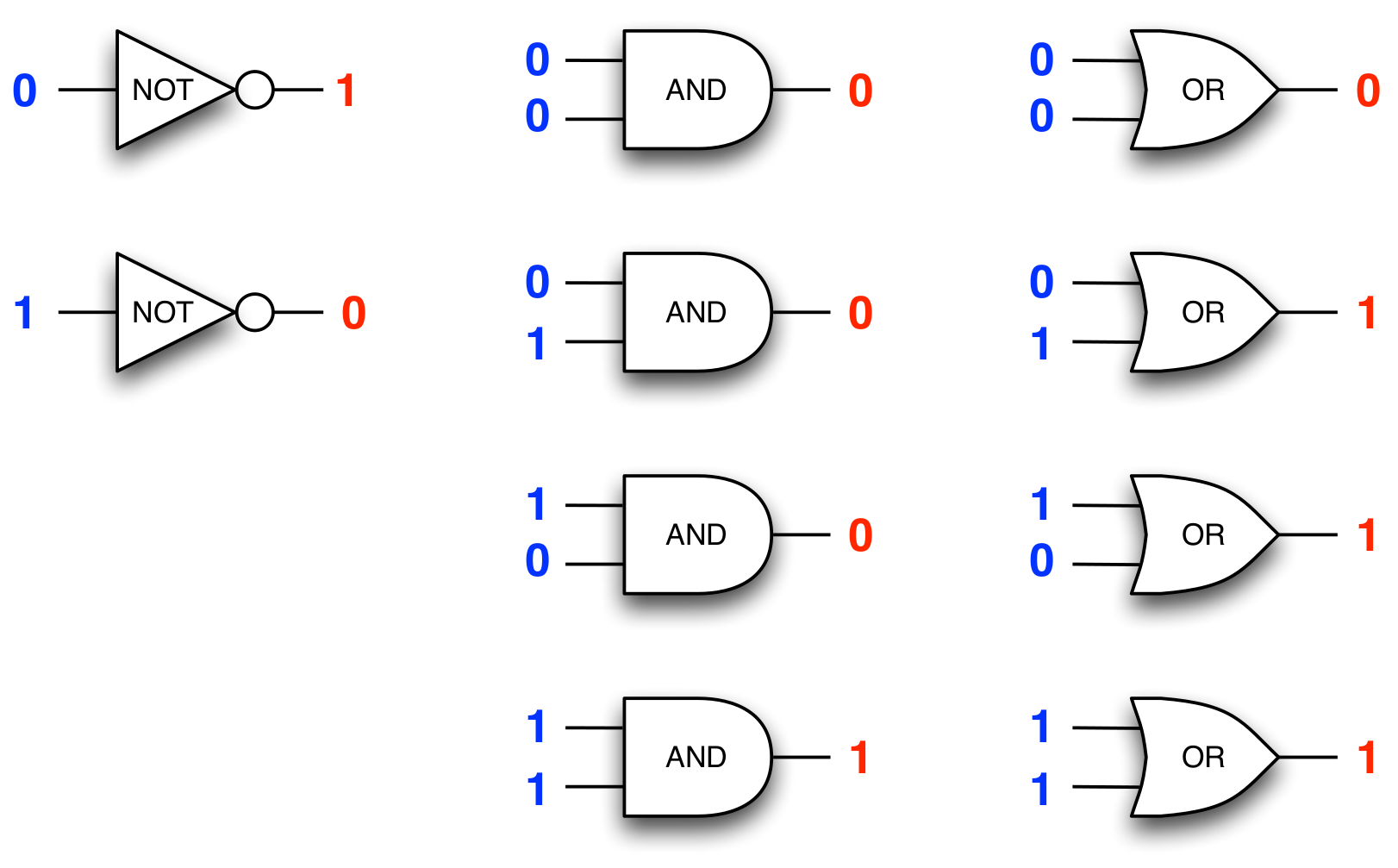
(The output (value) of a gate is determined by the inputs )
Logic gates - physical implementations
What kind of machines can be built by combining logic gates?
Circuits
- A combination of gates is called a circuit
- A circuit has inputs and output
- Compare this 'box' to a function…
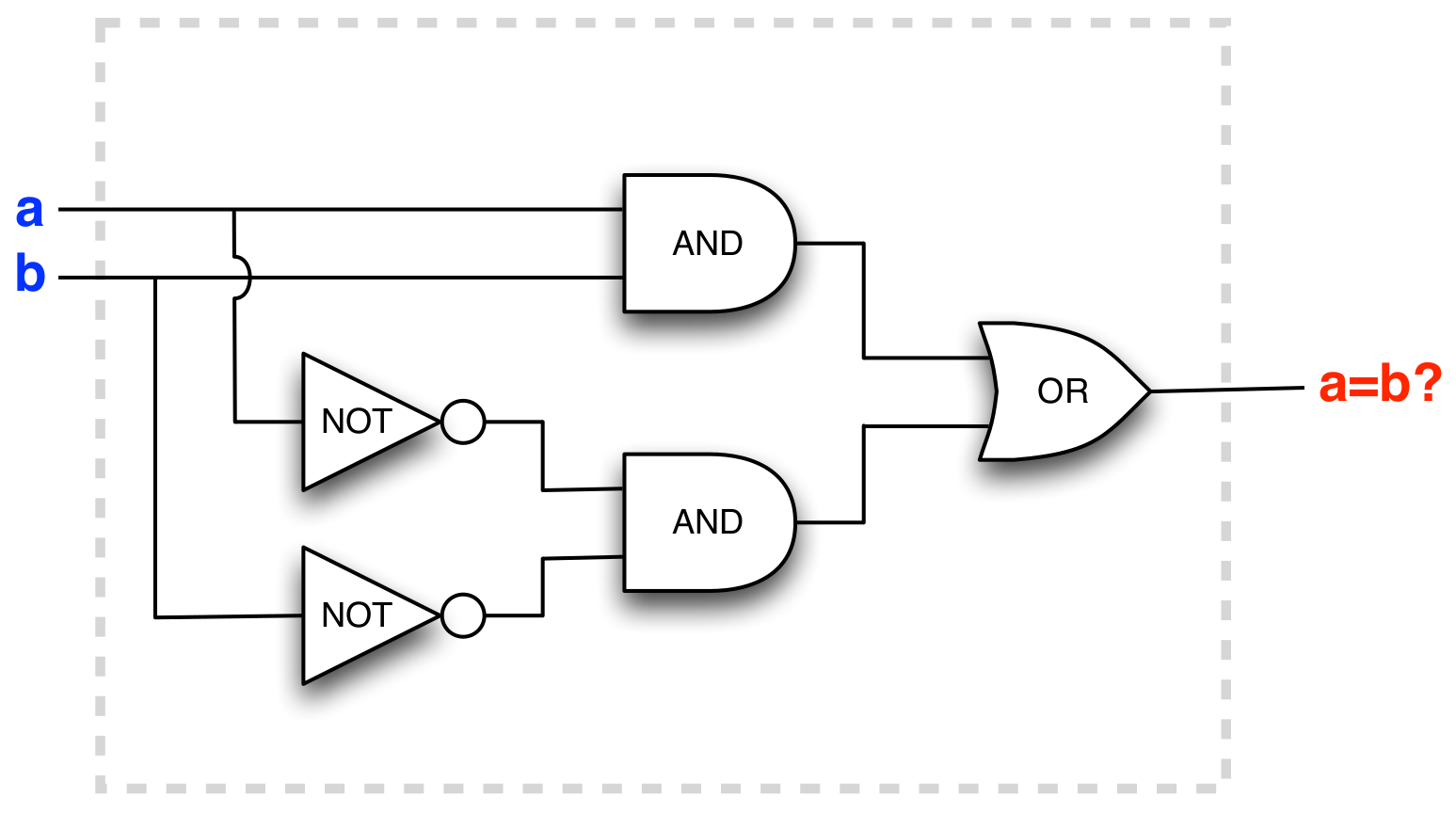
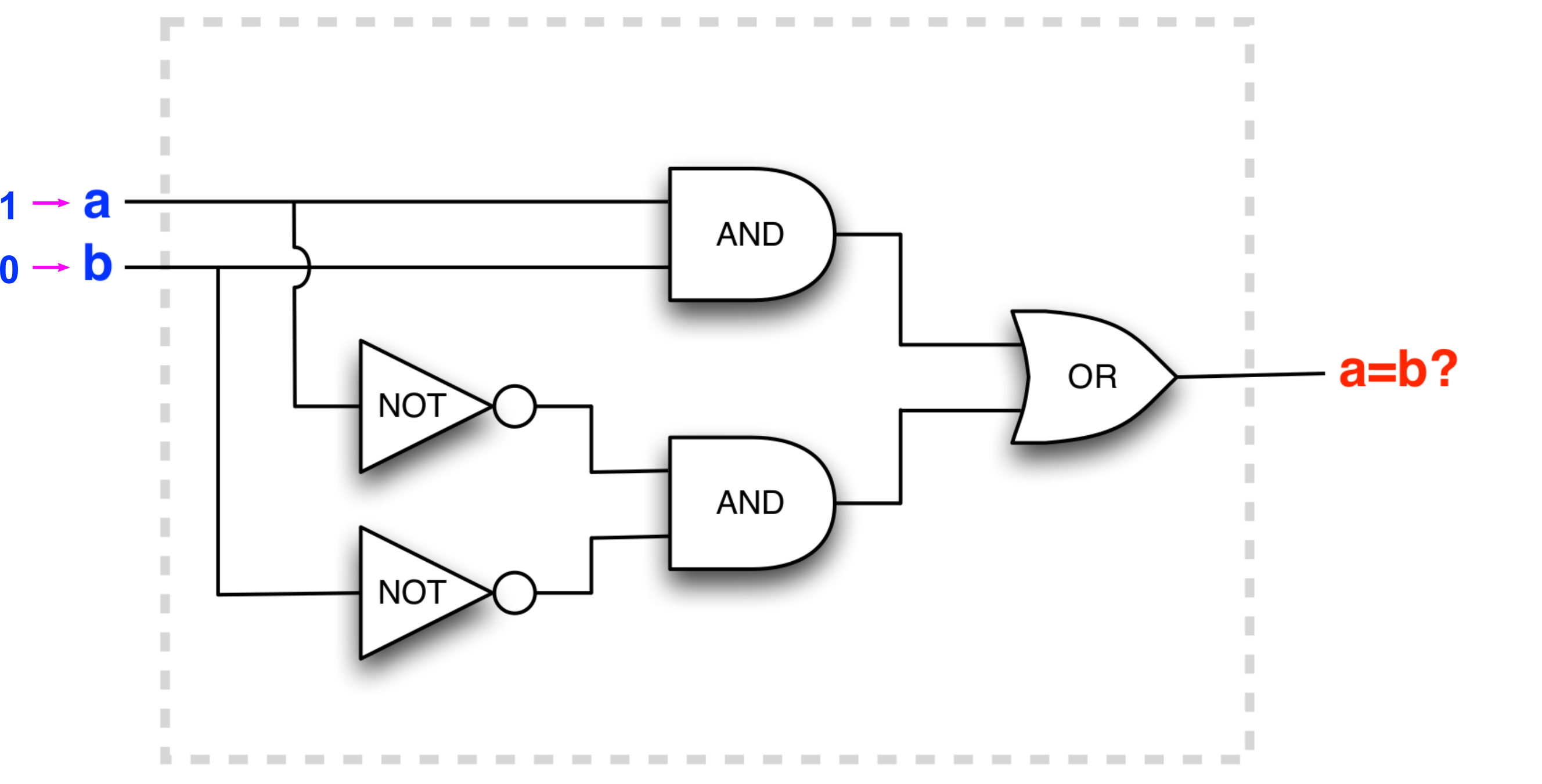
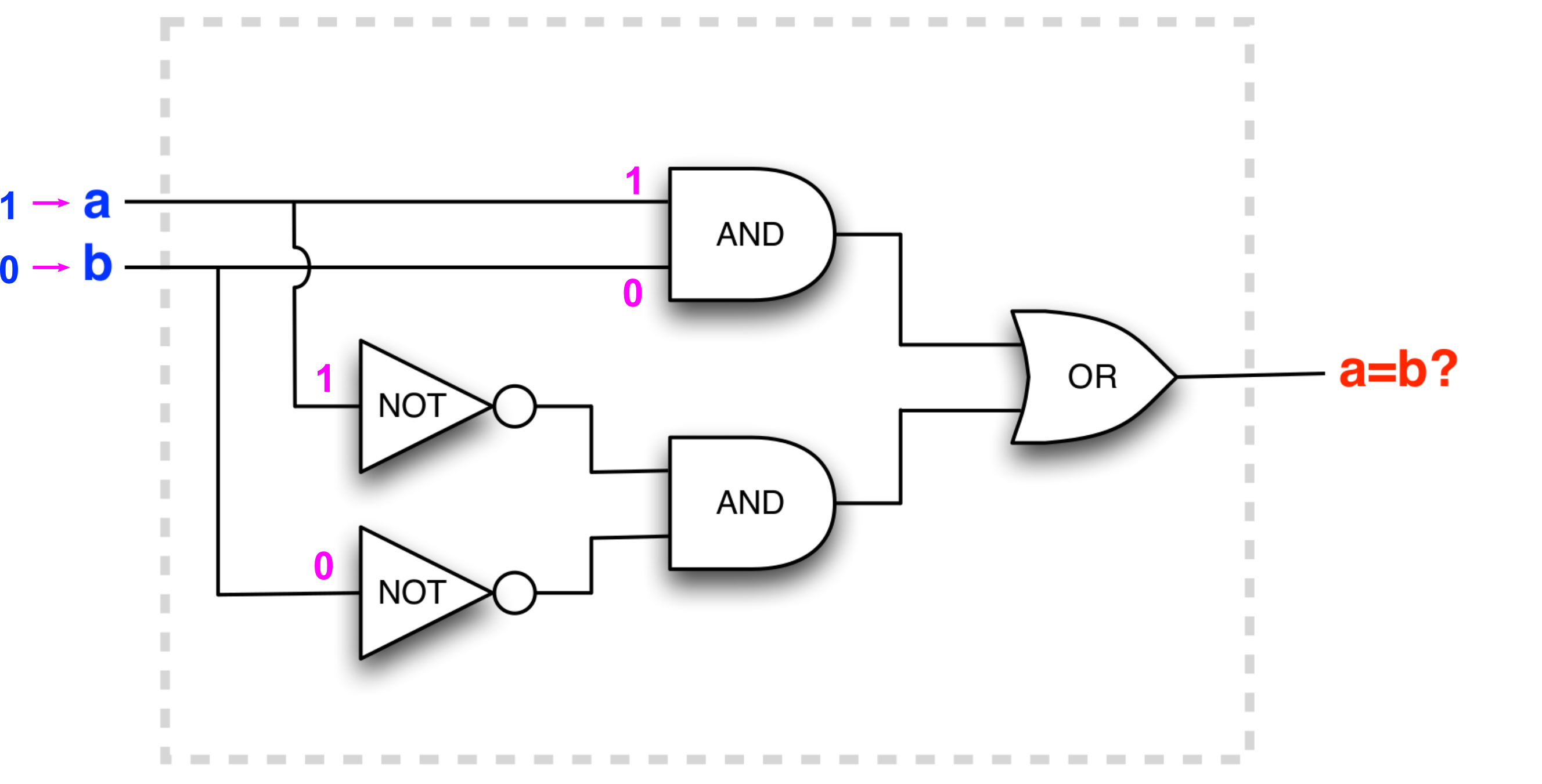
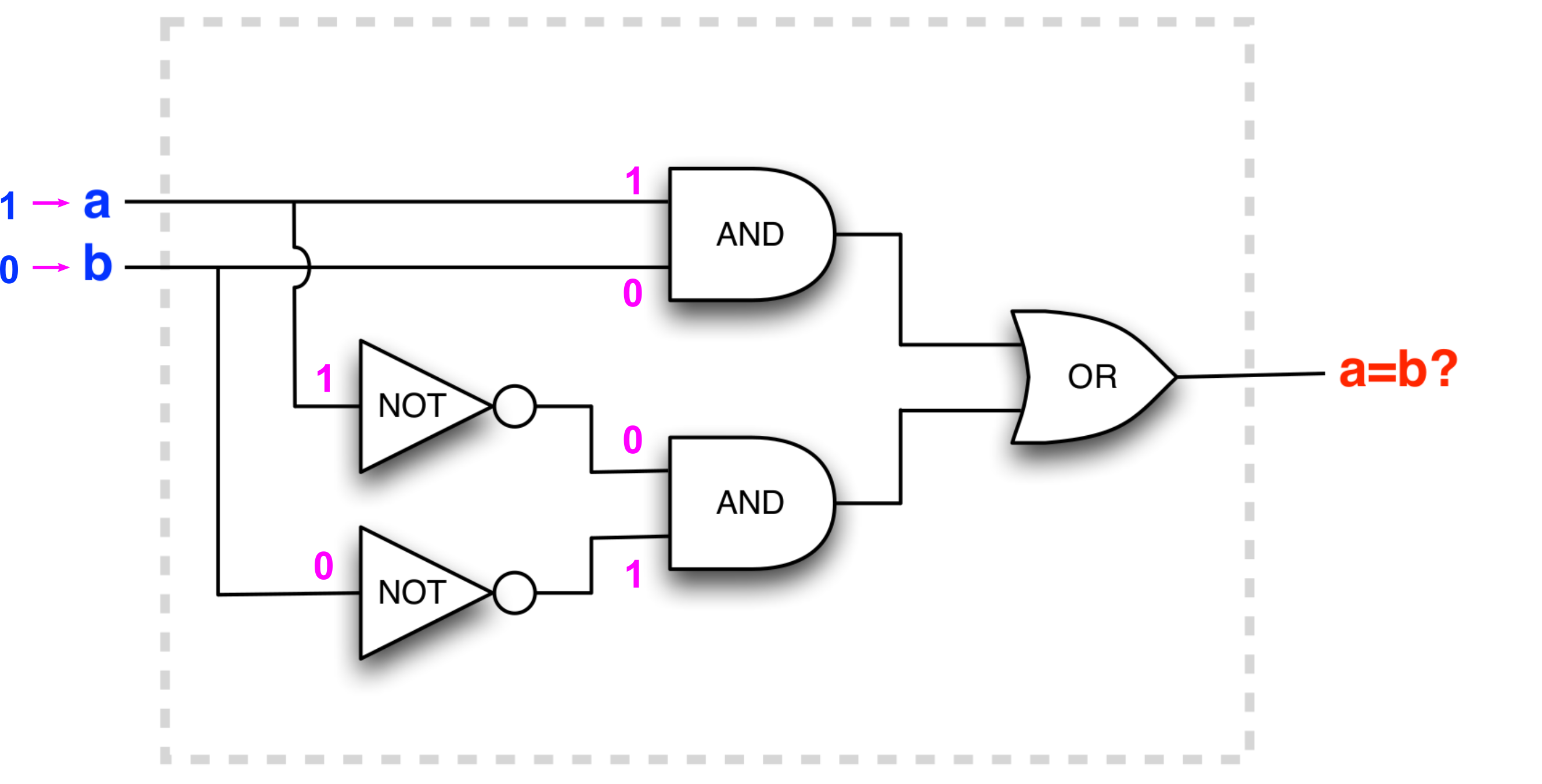
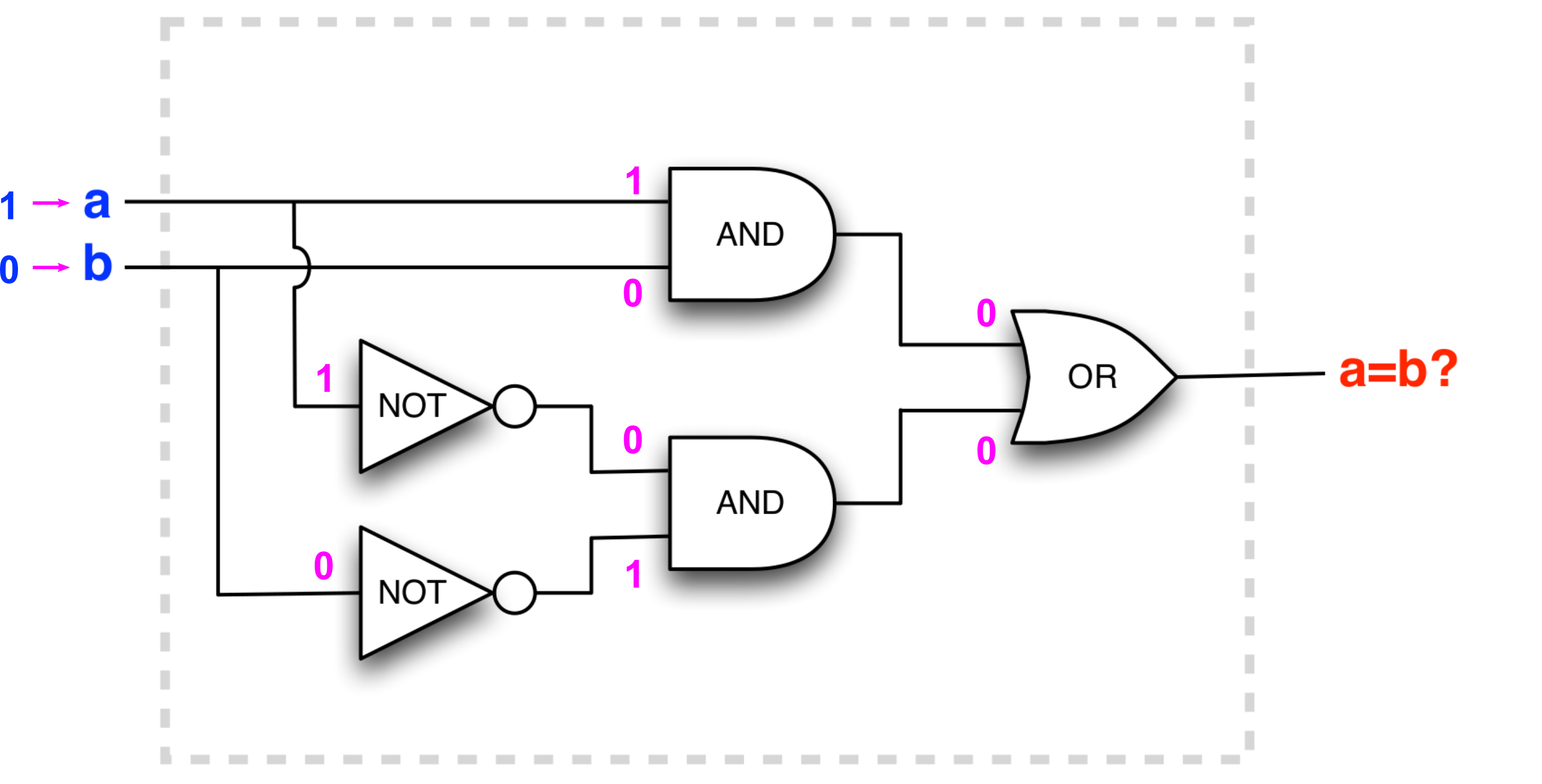
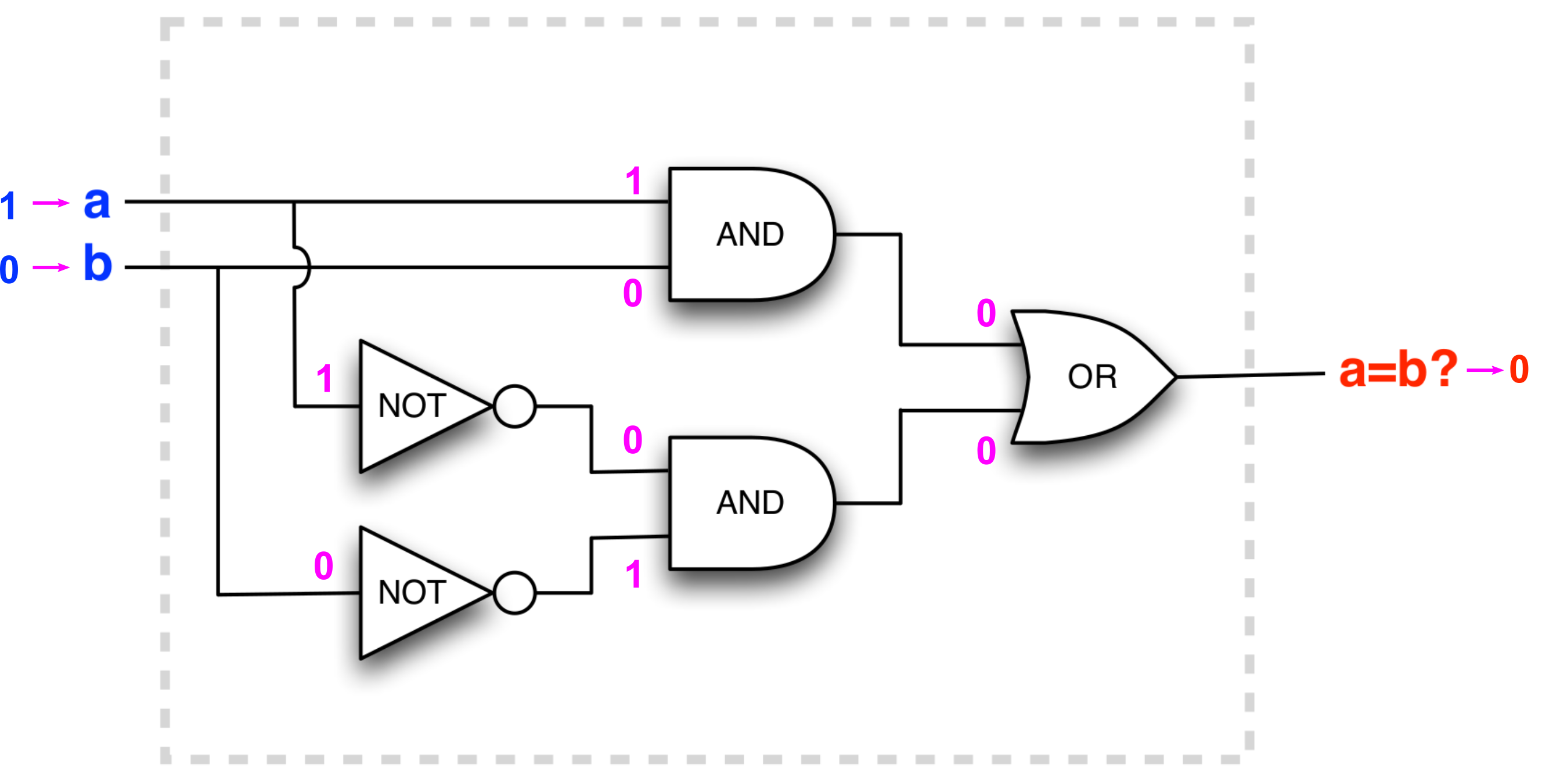
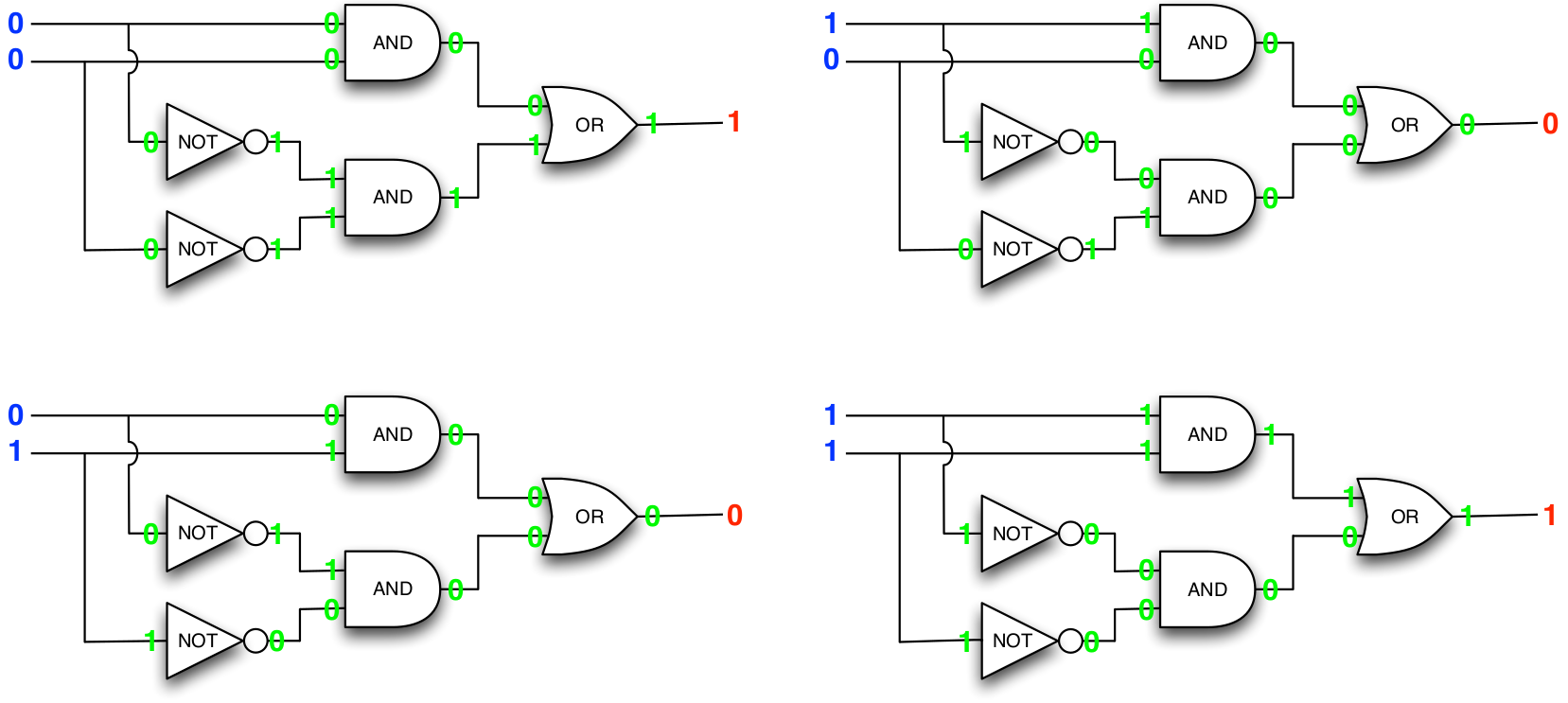
The circuit outputs changes with input !
Emulating circuits in Scala
Let's write a Scala programmer's construction kit for a circuit (and, later, a computer)!
We will need to represent:




What if we used objects…
to represent gates
as well as inputs.
And their inputs were 'previous' gates or input elements
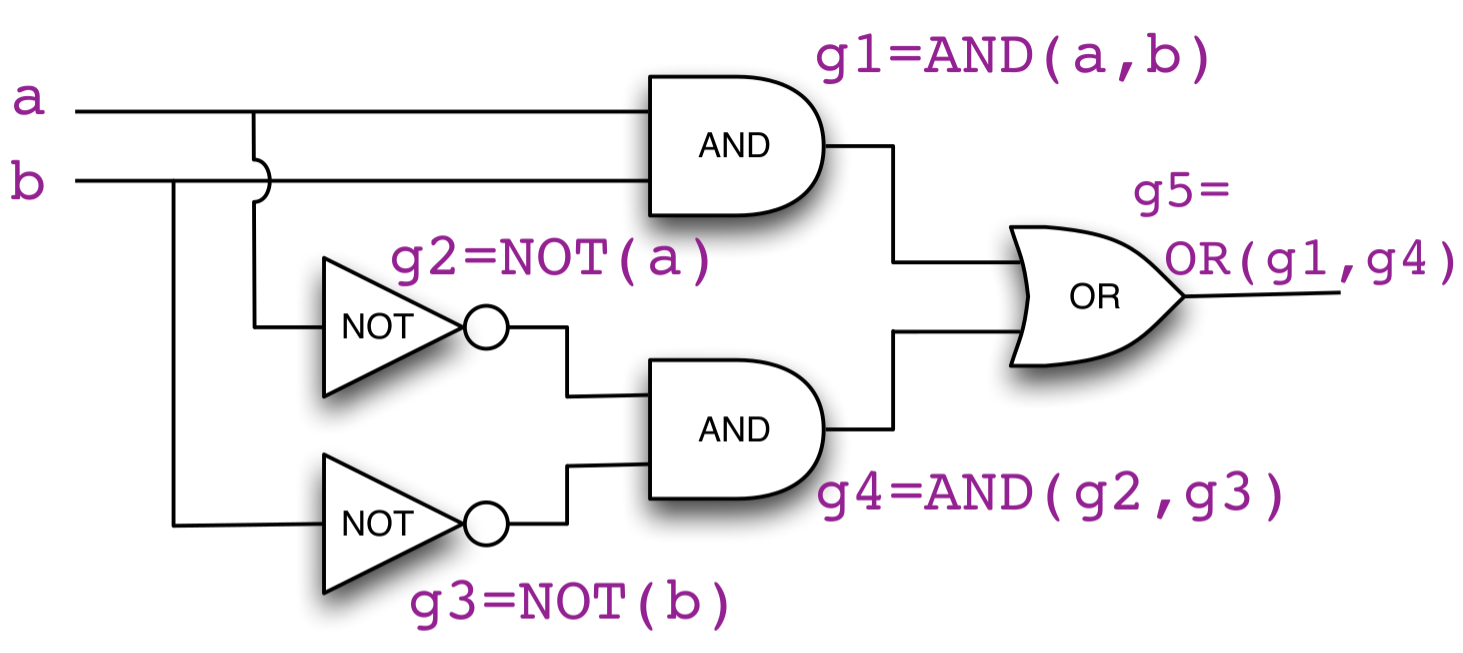
Then that should take care of the wiring.
And the 'output' is the value of the last gate object in the chain.
Making a Scala package: tinylog
package tinylog
Let's use common abstract class for logic gates and inputs
abstract class Gate():
def value: Boolean // implemented by the extending classes
end Gate
Implementing the logic gates
class NotGate(in: Gate) extends Gate():
def value = !in.value
end NotGate
class OrGate(in1: Gate, in2: Gate) extends Gate():
def value = in1.value || in2.value
end OrGate
class AndGate(in1: Gate, in2: Gate) extends Gate():
def value = in1.value && in2.value
end AndGate
And inputs
class InputElement() extends Gate():
var v = false // default value is false
def set(s: Boolean) = { v = s }
def value = v
end InputElement
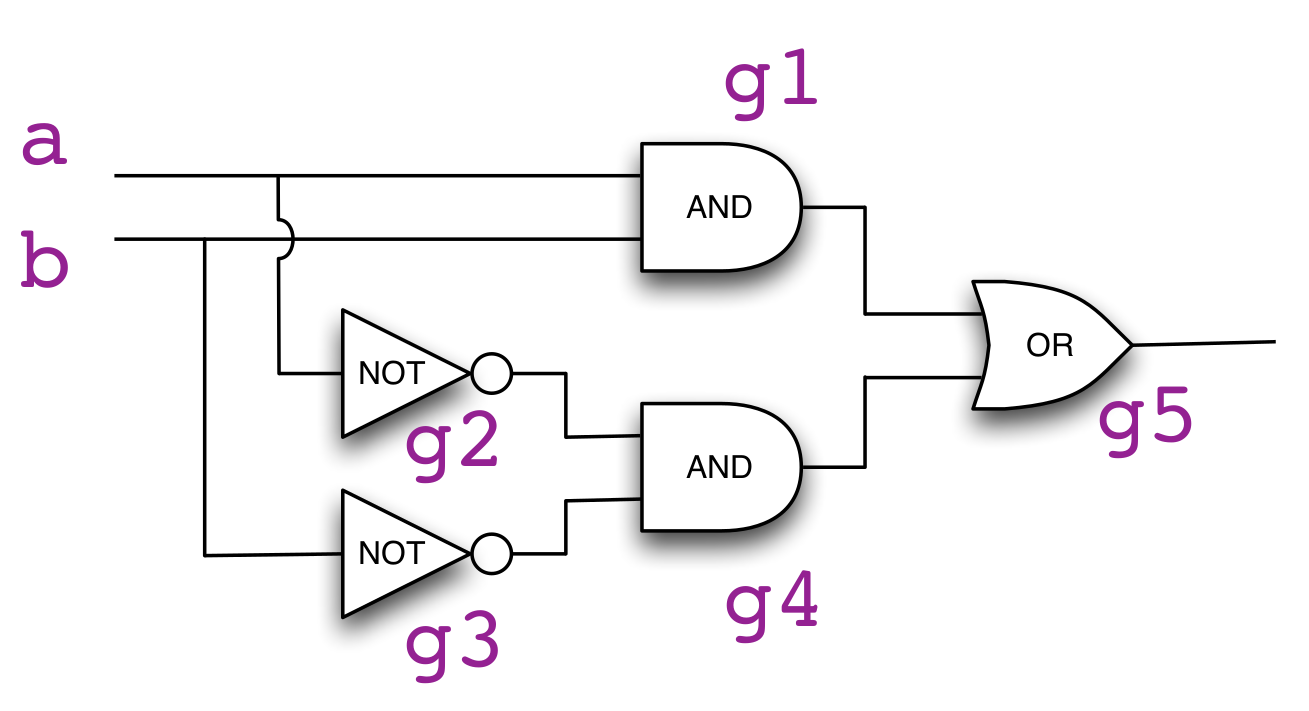
Building the example circuit in Scala
import tinylog.*
// Build a simple circuit
val a = new InputElement()
val b = new InputElement()
val g1 = new AndGate(a,b)
val g2 = new NotGate(a)
val g3 = new NotGate(b)
val g4 = new AndGate(g2,g3)
val g5 = new OrGate(g1,g4)

sbt tinylog/console from the round 3 exercise package.) Then we can test it:
scala> a.set(true)
scala> b.set(false)
scala> g5.value
val res5: Boolean = false
scala> a.set(false)
scala> b.set(false)
scala> g5.value
val res8: Boolean = true
Note how the circuit works as a function - when we change the input it 'recalculates' the output.
Improving syntax by specifying operators
- Scala allows us to define our own operators (such as
&&||+-/…) for classes - In this case it would make sense to have
&&,||,!act as short-cuts for AND, OR, and NOT gates
We extend our abstract Gate class somewhat:
class Gate():
/** Boolean value of the Gate.*/
def value: Boolean
/** Operator definition for NotGate of this Gate.*/
def unary_! = new NotGate(this)
/** Operator definition for AndGate of this Gate and that Gate.*/
def &&(that: Gate): Gate = new AndGate(this, that)
/** Operator definition for OrGate of this Gate and that Gate.*/
def ||(that: Gate): Gate = new OrGate(this, that)
end Gate
Using the operators

Now we can do:
import tinylog.*
// Build a simple circuit
val a = new InputElement()
val b = new InputElement()
val g1 = a && b
val g2 = !a
val g3 = !b
val g4 = g2 && g3
val g5 = g1 || g4
Or even:
import tinylog.*
// Build a simple circuit
val a = new InputElement()
val b = new InputElement()
val g5 = (a && b) || (!a && !b)
Scala creates the objects implicitly. Makes it easy to build large circuits.
Fine, but how do we create a machine that adds up numbers?
Let's start with a machine that adds up two single bit numbers
Adding up two single-bit numbers
Binary addition
\(0 + 0 = 0\)
\(0 + 1 = 1\)
\(1 + 0 = 1\)
\(1 + 1 = 10\)
Remember school: when the sum cannot 'fit' in a position we carry to the next.
Writing out the carry in all additions
\(0 + 0 = 00\)
\(0 + 1 = 01\)
\(1 + 0 = 01\)
\(1 + 1 = 10\)
To solve
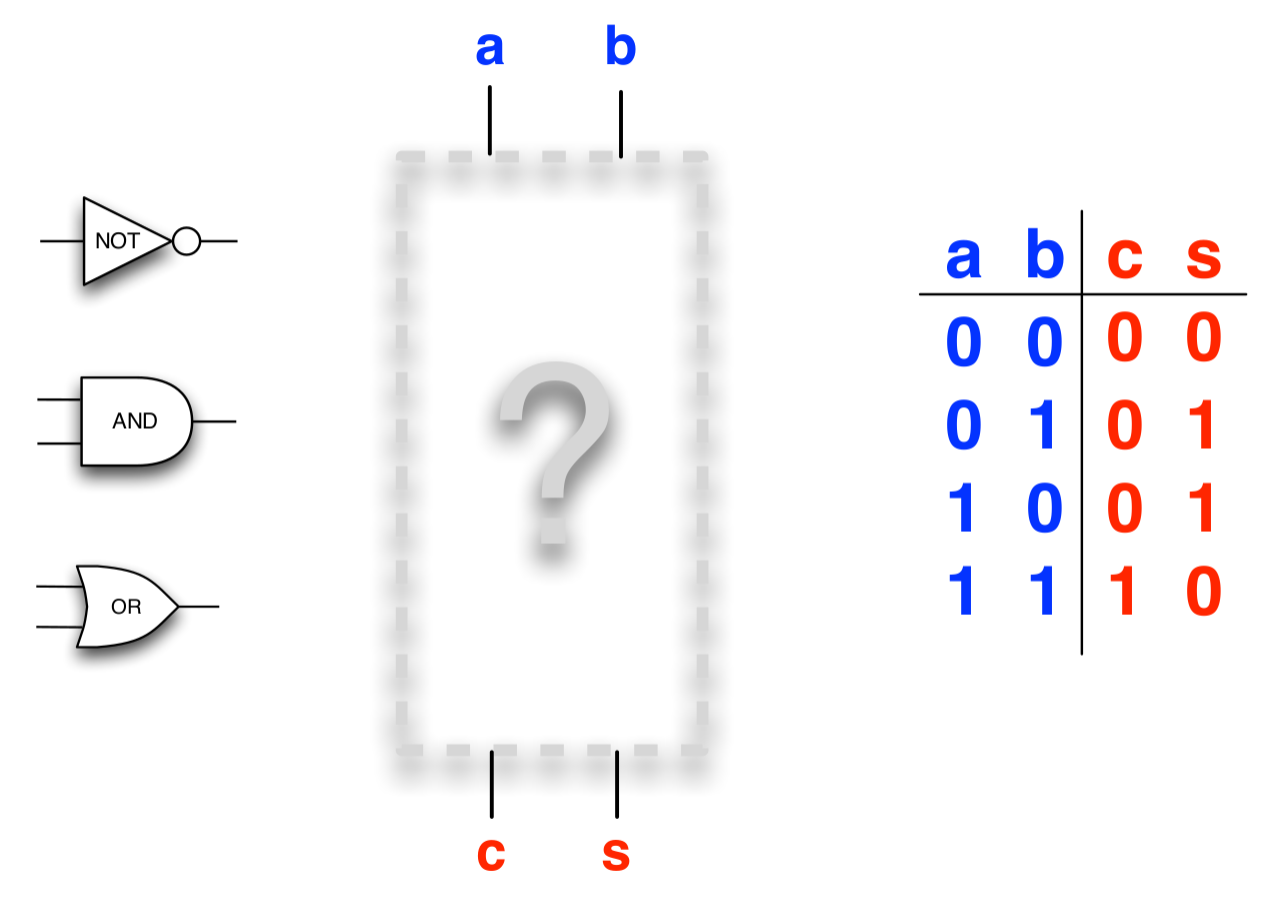
Which circuit performs the one-bit addition?

Discuss in pairs
Synthesis ?
Synthesis from truth table(s)
- In every row with output 1 write an AND operation which is true exactly when the inputs have the values of that row
- Combine these expressions to one long OR expression

(Assuming the inputs (a, b) are tinylog Gate, then Scala will automatically create the circuit with these expressions!)
Synthesis example: selector (multiplexer)
- Assume we want to switch between two bits
aandb, using a selector bits:- If the selector,
s, is \(0\) we want the output,r, to have the same value asa, and if it is \(1\) the output should have the same value asb
- If the selector,

We can build machines that compute with bits
A general procedure: Set up the truth table → build the formula
- But… How large are these circuits actually?
- What if we build a machine to add two 64 bit integers?
- \(2 \times 64 = 128\) inputs
- Meaning that the truth table has \(2^{128} = 340282366920938463463374607431768211456\) rows
- Ouch, we need to be smarter
Building more complicated circuits
- Work with a bus
- Carries word of multiple bits instead of wires with a single bit
- Better understanding of the specific task at hand could give insights in a better circuit design
Implementation of a Bus class in tinylog
- A
Busrepresents multiple bits (gates), so let's make it extend the Scala traitSeq- Meaning that
Busis a custom Scala collection forGateobjects
- Meaning that
- We'll also give it both bus-level operators for AND, OR, NOT (
&,|,~)- Recall the word-operations last round
You can read more about how Bus is constructed in the course notes, and find the source of Bus.scala in the tinylog sub-project of this round's exercises.
Because Bus is a Seq we have access to the usual methods for collections, such as map and fold.
Example: building a bus selector
A circuit that gives the value of bus aa if s is 0 and bb if s is 1:
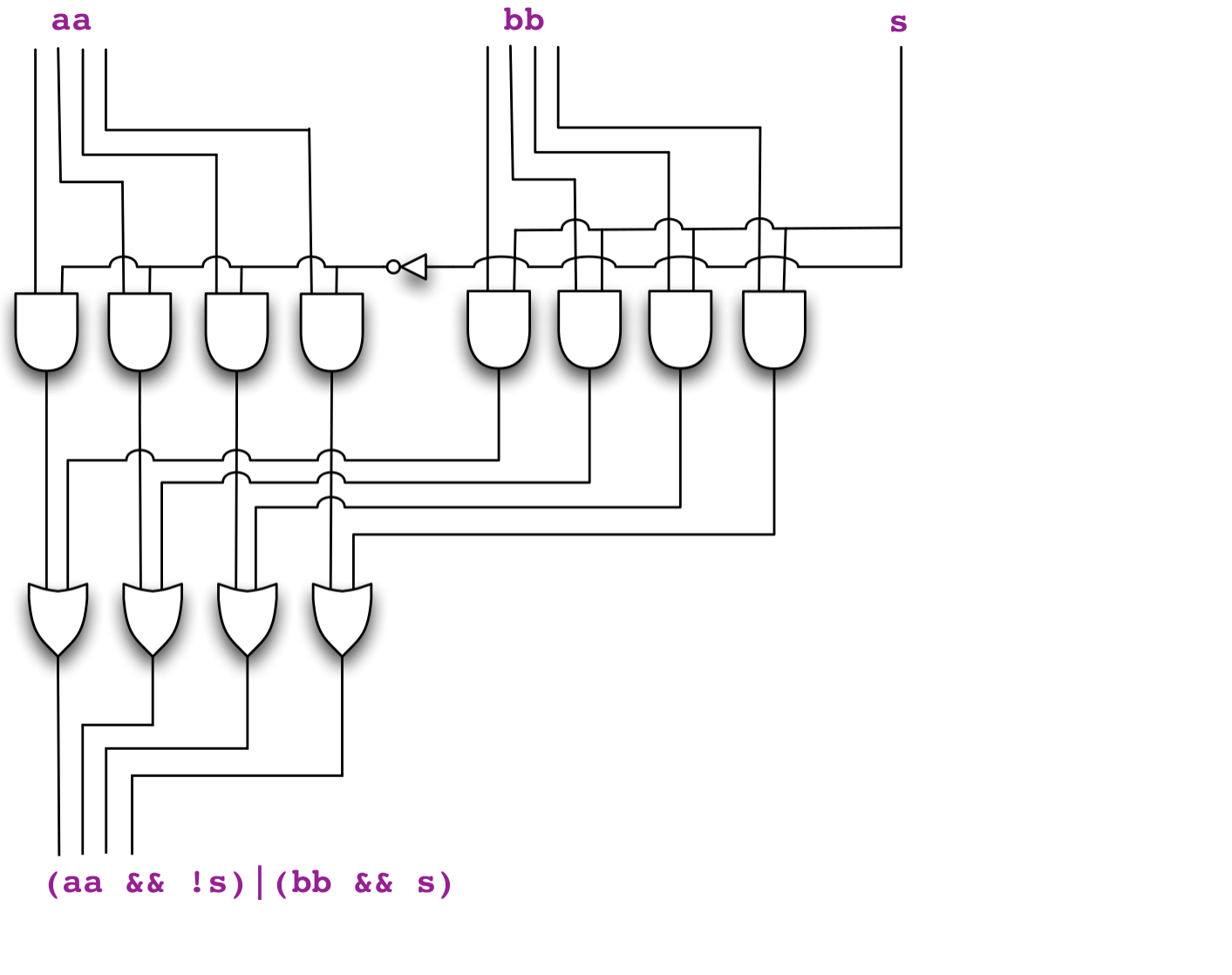
In Scala:
scala> import tinylog.*_
scala> val aa = Bus(Gate.False, Gate.True, Gate.True, Gate.True)
scala> val bb = Bus(Gate.True, Gate.False, Gate.False, Gate.False)
scala> val s = Gate.input() // Use an input gate so we can select
scala> val cc = (aa && !s) | (bb && s) // Construct the circuit
scala> cc.values // By default s is false, so we will select aa
val res0: Seq[Boolean] = List(false, true, true, true)
scala> s.set(true) // But, by setting s to true...
scala> cc.values // The circuit output has changed to bb
val res2: Seq[Boolean] = List(true, false, false, false)
Toggler to display an UI:
scala> val t = new Toggler() // Create toggler UI
scala> t.watch("aa",aa) // Display bus aa
scala> t.watch("bb",bb) // Display bus bb
scala> t.watch("s",s) // Display selector bit
scala> t.watch("cc", cc) // Display output bus cc
scala> t.go() // And start
You can see a demonstration of a similar example here
Example: Palindrome
Task: write a function that creates a circuit detecting if a Bus contains a bit-palindrome.
- First, it can be a good idea to sketch a 'circuit' describing what we want to do.
- "Check if first gate is equal to last, check if second gate is equal to second last…"
- If all these checks are true then we have a palindrome
- Is there some operation we have not expressed using Boolean logic?
- Yes, the equality check
=? - But we know how!
(a && b) || (!a && !b)
- Yes, the equality check
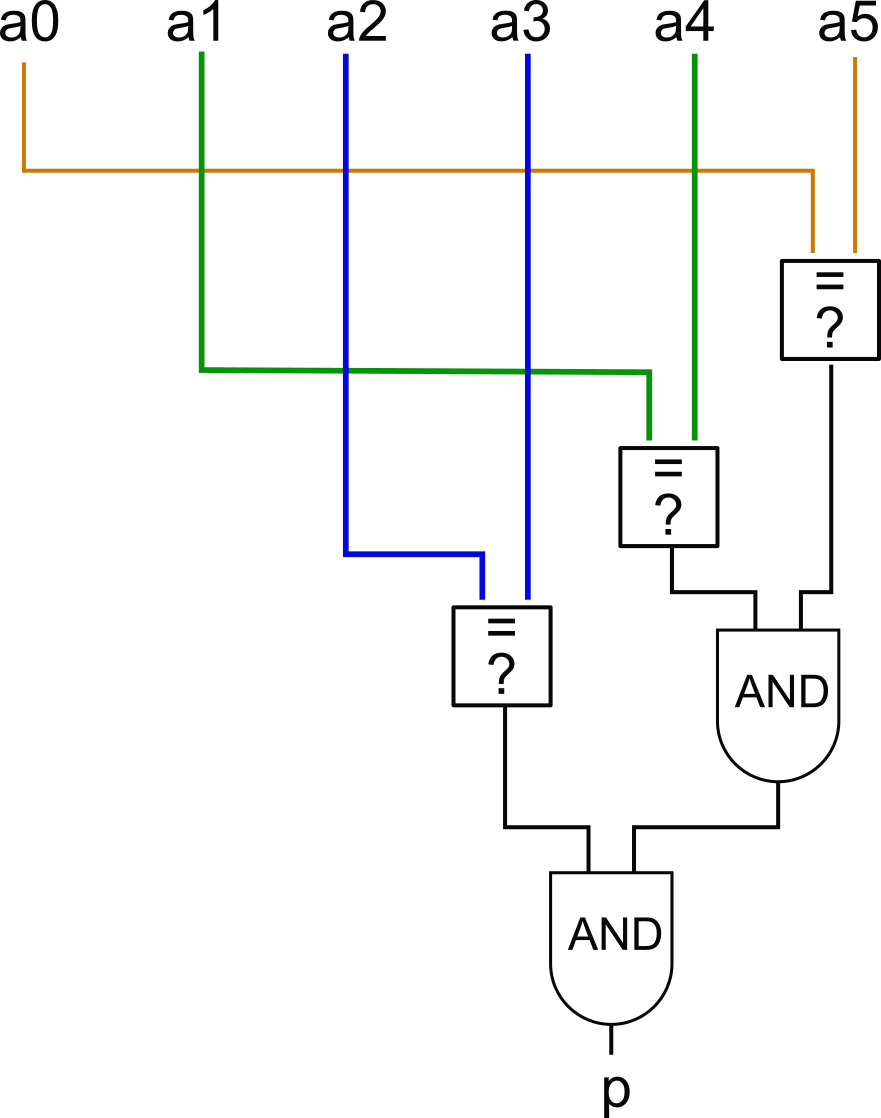
10101 is a palindrome; 11001 is not.) Example: Palindrome
// Helper function - output gate is true when input
// gates are equal
def gatesEqCircuit(a : Gate, b : Gate) : Gate =
(a && b) || (!a && !b)
// Output gate is true when input bus is a palindrome
def isPalindromeCircuit(aa: Bus) : Gate =
val len = aa.length
// Create an array of size len/2 to hold the eq gates
val eqc = new Array[Gate](len/2)
for i <- 0 until len/2 do
eqc(i) = gatesEqCircuit(aa(i), aa(len-1-i))
end for
// Now we can just reduce it with AND to form the
// final gate
eqc.reduce(_ && _)
end isPalindromeCircuit
val aa = Bus.inputs(7)
val p = isPalindromeCircuit(aa)
val t = new Toggler()
t.watch("Input",aa)
t.watch("Palindrome?",p)
t.go()

NOTE: At no point does the code need to check the value of a gate when we build the circuit!
What does the following code achieve?
import tinylog.*
def e(a:Gate, b:Gate) = (a && b) || (!a && !b)
def f(aa:Bus, bb:Bus) =
require(aa.length == bb.length)
val x = aa.zip(bb).map((a,b) => e(a,b))
x.reduce(_ && _)
end f
Fine, but…
What about a 64 bit machine that adds up two 64 bit numbers?
What exactly do we do when adding up two integers?
Back to School in base 10
Back to School in base 2

Addition is easy in binary!
Build a circuit that follows the procedure, one significant bit at a time.
- Every significant number is determined by adding up three numbers
- In binary, each are either
0or1.
- In binary, each are either
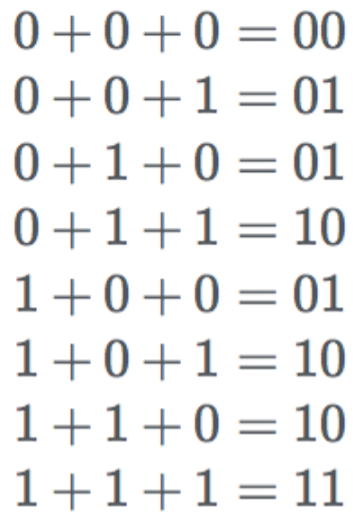
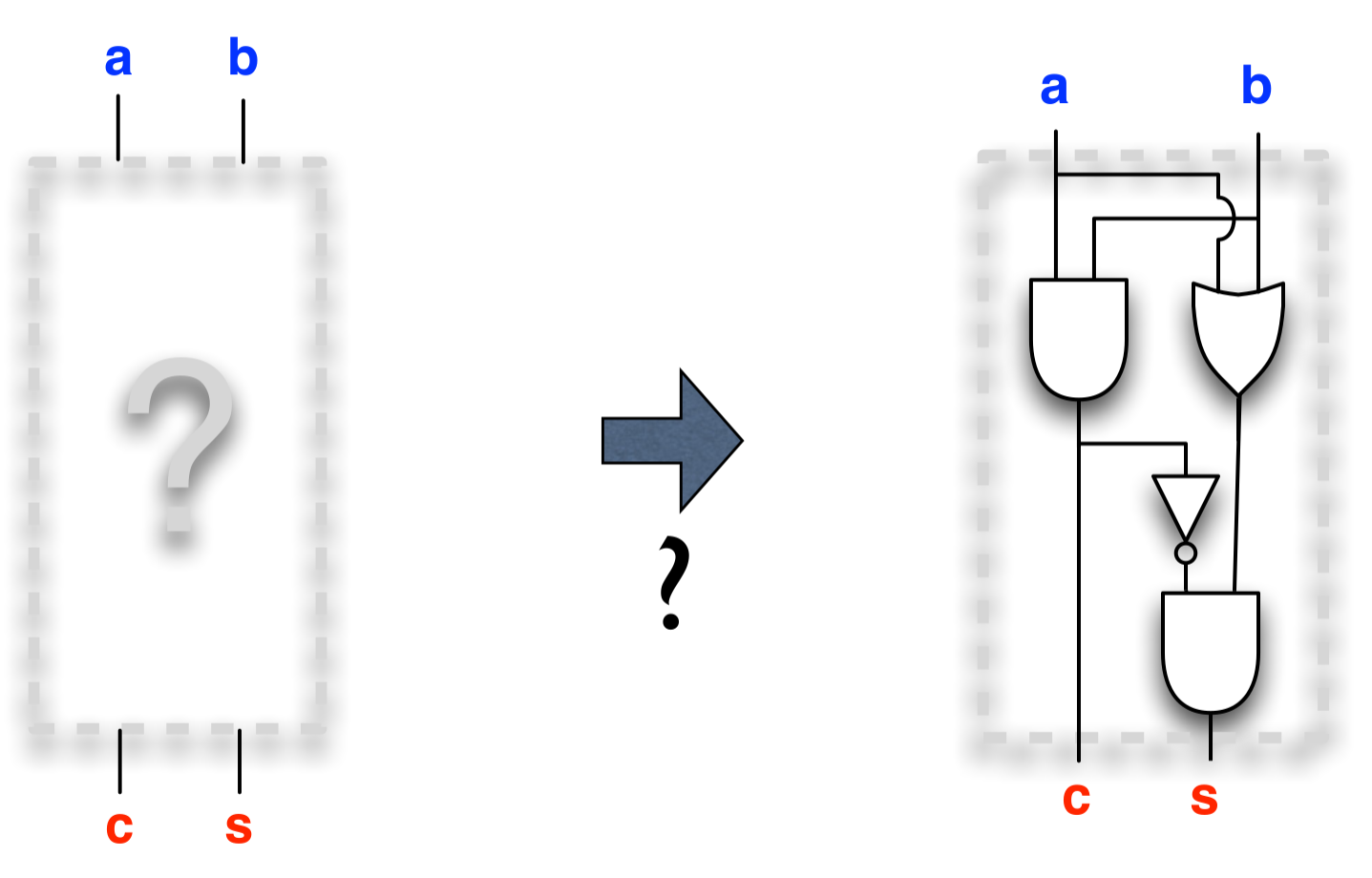
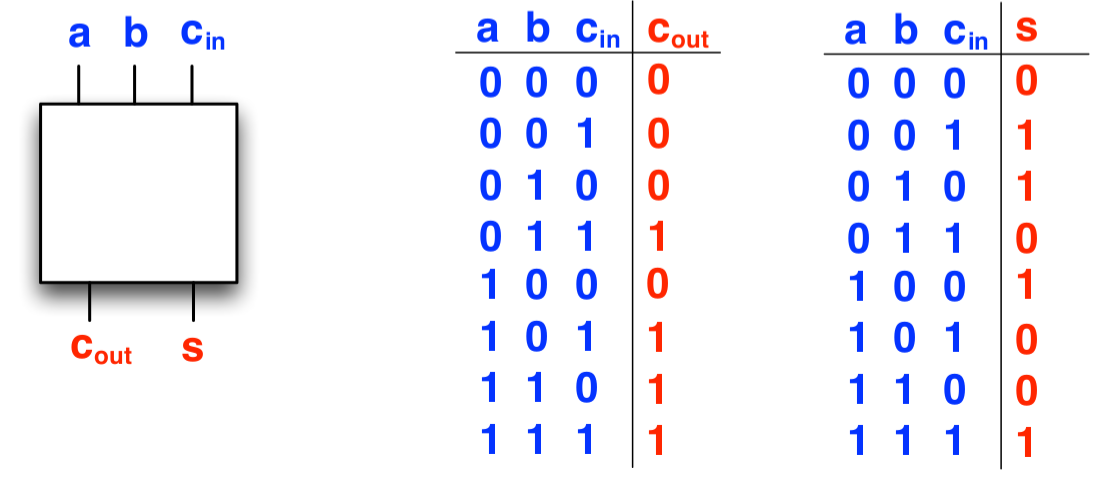
The Full adder
Call this circuit a Full adder
The Ripple-carry adder
- Connect the Full adder module one significant bit (starting with least significant) at a time
- Called a Ripple-carry adder because the carry bits spread out like ripples on a surface of water
Implementation:
def buildFullAdder(a: Gate, b: Gate, c_in: Gate): (Gate, Gate) =
val c_out = (!a && b && c_in) || (a && !b && c_in) || // ...
(a && b && !c_in) || (a && b && c_in)
val s = (!a && !b && c_in) || (!a && b && !c_in) || // ...
(a && !b && !c_in) || (a && b && c_in)
(c_out, s)
end buildFullAdder
def buildRCAdder(bus1: Bus, bus2: Bus) =
require(bus1.length == bus2.length,
"Can only add buses of same length")
var carry_in: Gate = Gate.False // no initial carry
val ss = new Array[Gate](bus1.length)
for i <- 0 until bus1.length do
val (carry_out, sum) = buildFullAdder(bus1(i), bus2(i),
carry_in)
carry_in = carry_out // carry from bit i propagates
ss(i) = sum
end for
new Bus(ss.toIndexedSeq)
end buildRCAdder
Example: 4 bit addition machine
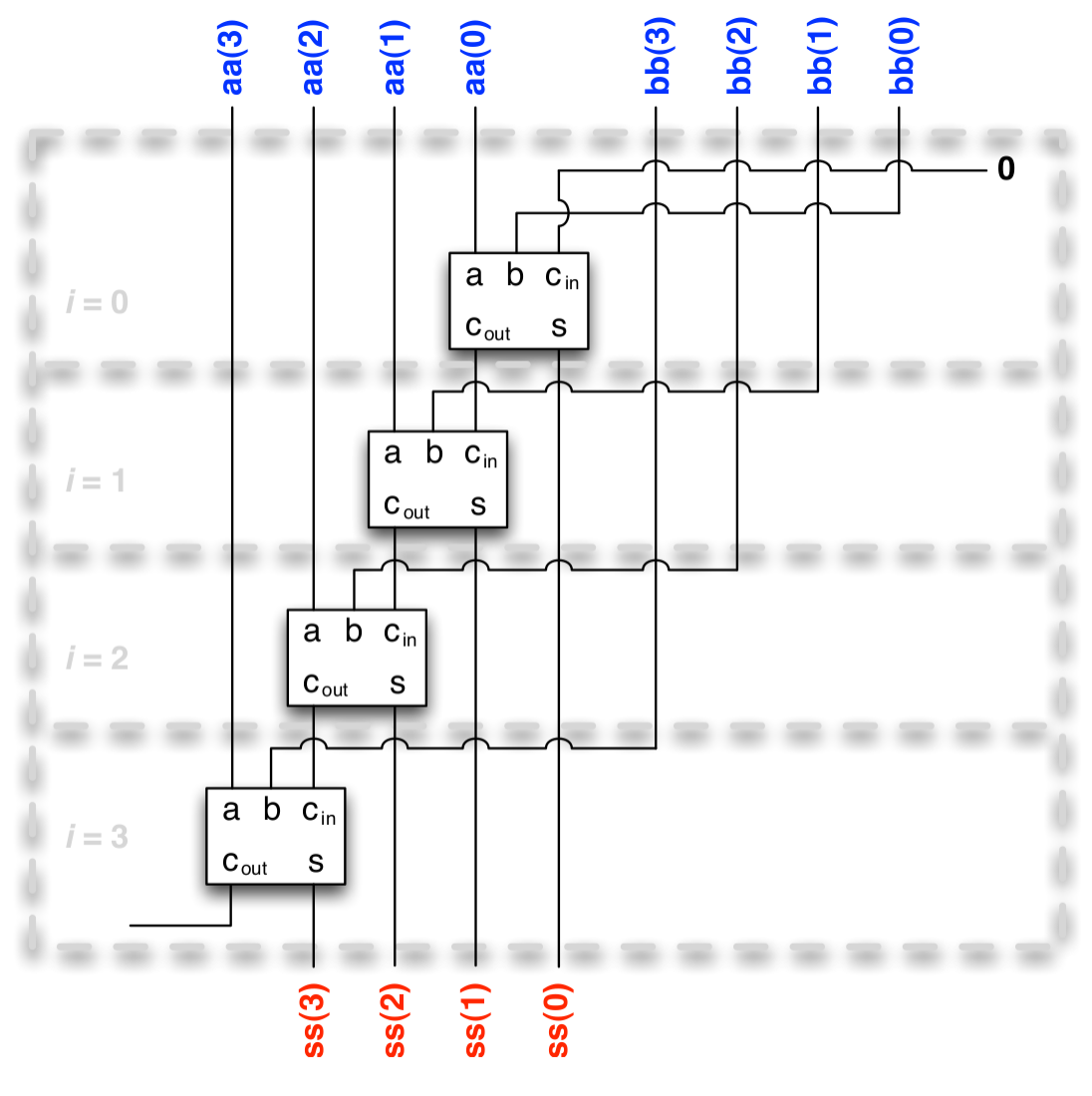
Gotcha when interpreting a Bus as a data word
Sequences are usually though of as indexed 'from left to right', but (binary) numbers are indexed (least significant digit) 'from right to left'.
For example, this constant three gate bus:
val aa = Bus(Gate.True, Gate.True, Gate.False)
represent the binary string 011.
Common pitfall when debugging exercises for example.
Exercises
This week:
- Gate expressions
- Two basic operations with
Gate
- Two basic operations with
- Operations on Circuits
- Different operations using circuits
- Note that count true bits cannot be implemented in the same way as in round 2
- Bus writer
- Build a circuit that selects a bus and writes data to it
- (Challenge problem: Shallow operations)
Hints:
- Drawing the circuit helps to figure out what to do
- These exercises are all about building circuits from
GateandBususing boolean operations - The values of
Gate(andBus) are not known when the circuit is constructed!- If you ever find yourself wanting to check the value of a
GateorBuswhen you build the circuit, your design is probably wrong - Instead use the Boolean operators for
GateandBus- these are re-evaluated every time the input changes
- If you ever find yourself wanting to check the value of a
- The circuits and bus write exercises come with
*Play.scalamain programs- Skeleton code using
Triggerfor you to edit and play around with
- Skeleton code using

