Efficiency

After this round, you

• can provide examples of computational resources
• can measure program run-time in Scala
• know the mathematical definitions of \(\mathcal{O}\), \(\Omega\), and \(\Theta\)
• can define Big-O for program running times, and
  • analyse a basic program in this respect
• have experience of indexing and searching
• can implement and use binary search

Efficiency ?

• Why does the efficiency of a program matter?
• How (in what terms) can it be defined?

Discuss in pairs https://presemo.aalto.fi/prog2

Computation takes resources

Efficiency aim

We want the amount of needed resources scale well when the input instance grows in size.

Instance = problem description ≅ input data

• For example:
  • The size of an image
  • Number of elements in a matrix
  • The number of users (in DB, or connected to server, or…)
  • Number of AI controlled characters in a game
  • …

Time

In this course we will (mostly) focus on time efficiency.

Measuring the running time

Different ways of measuring the running time of a program:

• Wall clock time (= Elapsed time) : time measured by an "external clock" (Note that if there are other resource intensive programs running on the computer the measured program needs to wait.)
• CPU time: time spent by the CPU running the program, subdivided into
  • User time: time that is spent on the program code
  • System time: time that is spent on system calls made by the program (I/O, etc)

In the following we will focus on measuring CPU time.

Measuring CPU time in Scala

• Scala System.nanoTime gives Wall Clock time
• Instead, we use ThreadMXBean from java.lang.management for CPU Time
  • Important: nanosecond precision but not accuracy
• So, use repeated measurements to improve accuracy
• We can define Scala functions
  • getCPUTime
  • measureCpuTime
  • measureCpuTimeRepeated

Getting current CPU time in Scala

import java.lang.management.{ ManagementFactory, ThreadMXBean }
val bean: ThreadMXBean = ManagementFactory.getThreadMXBean()

def getCpuTime: Long =
  if bean.isCurrentThreadCpuTimeSupported() then
    bean.getCurrentThreadCpuTime()
  else
    0L

Measuring CPU time in Scala (once)

Measure once, good enough if we think the operation will take more than about 0.1 s.

/** Define minimum positive time greater than 0.0*/
val minTime = 1e-9 // Needed as Windows gives 0.0 on small durations

/**
 * Runs the argument function f and measures the user+system time spent in it in seconds.
 * Accuracy depends on the system, preferably not used for runs taking less than 0.1 seconds.
 * Returns a pair consisting of
 * - the return value of the function call and
 * - the time spent in executing the function.
 */
def measureCpuTime[T](f: => T): (T, Double) =
  val start: Long = getCpuTime
  val r = f
  val end: Long = getCpuTime
  val t: Double = minTime max (end - start) / 1e9
  (r, t)

Measuring CPU time in Scala (repeated)

Measure repeatedly and calculate average. Necessary for functions which will complete fast.

/**
 * The same as measureCpuTime but the function f is applied repeatedly
 * until a cumulative threshold time use is reached (currently 0.1 seconds).
 * The time returned is the cumulative time divided by the number of repetitions.
 * Therefore, better accuracy is obtained for very small run-times.
 * The function f should be side-effect free!
 */
def measureCpuTimeRepeated[T](f: => T): (T, Double) =
  val start: Long = getCpuTime
  var end = start
  var runs = 0
  var r: Option[T] = None
  while end - start < 100000000L do
    runs += 1
    r = Some(f)
    end = getCpuTime
  val t = minTime max (end - start) / (runs * 1e9)
  (r.get, t)

Let's get some data

scala> val data =
  for n <- Seq(10000000,20000000,
    30000000,40000000)
  yield measureCpuTimeRepeated {
    // Add up n first positive numbers
    (1 to n).foldLeft(0L)(_+_)
  }

val data: Seq[(Long, Double)] = List(
  (50000005000000,0.107851275),
  (200000010000000,0.191804696),
  (450000015000000,0.28604331),
  (800000020000000,0.379793504))

A more advanced example: Matrix operations

In our case \(n \times n\) square matrices, e.g. \[ A = \begin{pmatrix} a_{(0,0)} & a_{(0,1)} & \cdots & a_{(0,n-1)}\\ a_{(1,0)} & a_{(1,1)} & \cdots & a_{(1,n-1)}\\ \vdots & \vdots & \ddots & \vdots\\ a_{(n-1,0)} & a_{(n-1,1)} & \cdots & a_{(n-1,n-1)} \end{pmatrix} \]

Matrix sum and multiplication

Examples:

Simple Matrix class in Scala

/** Basic square matrix class.*/
class Matrix(val n: Int):
   require(n > 0, "The dimension n must be positive")
   protected[Matrix] val entries = new Array[Double](n * n)

   /** With this we can access elements by writing M(i,j) */
   def apply(row: Int, column: Int) =
     require(0 <= row && row < n)
     require(0 <= column && column < n)
     entries(row * n + column)
   end apply

   /** With this we can set elements by writing M(i,j) = v */
   def update(row: Int, column: Int, value: Double) : Unit =
     require(0 <= row && row < n)
     require(0 <= column && column < n)
     entries(row * n + column) = value
   end update

   //... More methods to come ...

Matrix addition in Scala

class Matrix //... as before

    /** Returns a new matrix that is the sum of this and that */
    def +(that: Matrix): Matrix =
        val result = new Matrix(n)
        for row <- 0 until n; column <- 0 until n do
            result(row, column) = this(row, column) + that(row, column)
        result
    end +

Rule: \(c_{(i,j)} = a_{(i,j)} + b_{(i,j)}\)

Matrix multiplication in Scala

class Matrix //... as before

    /** Returns a new matrix that is the product of this and that */
    def *(that: Matrix): Matrix =
      val result = new Matrix(n)
      for row <- 0 until n; column <- 0 until n do
        var v = 0.0
        for i <- 0 until n do
          v += this(row, i) * that(i, column)
        result(row, column) = v
      end for
      result
    end *

Rule: \(c_{(i,j)} = \sum_{k=0}^{n-1} a_{(i,k)} \times b_{(k,j)}\)

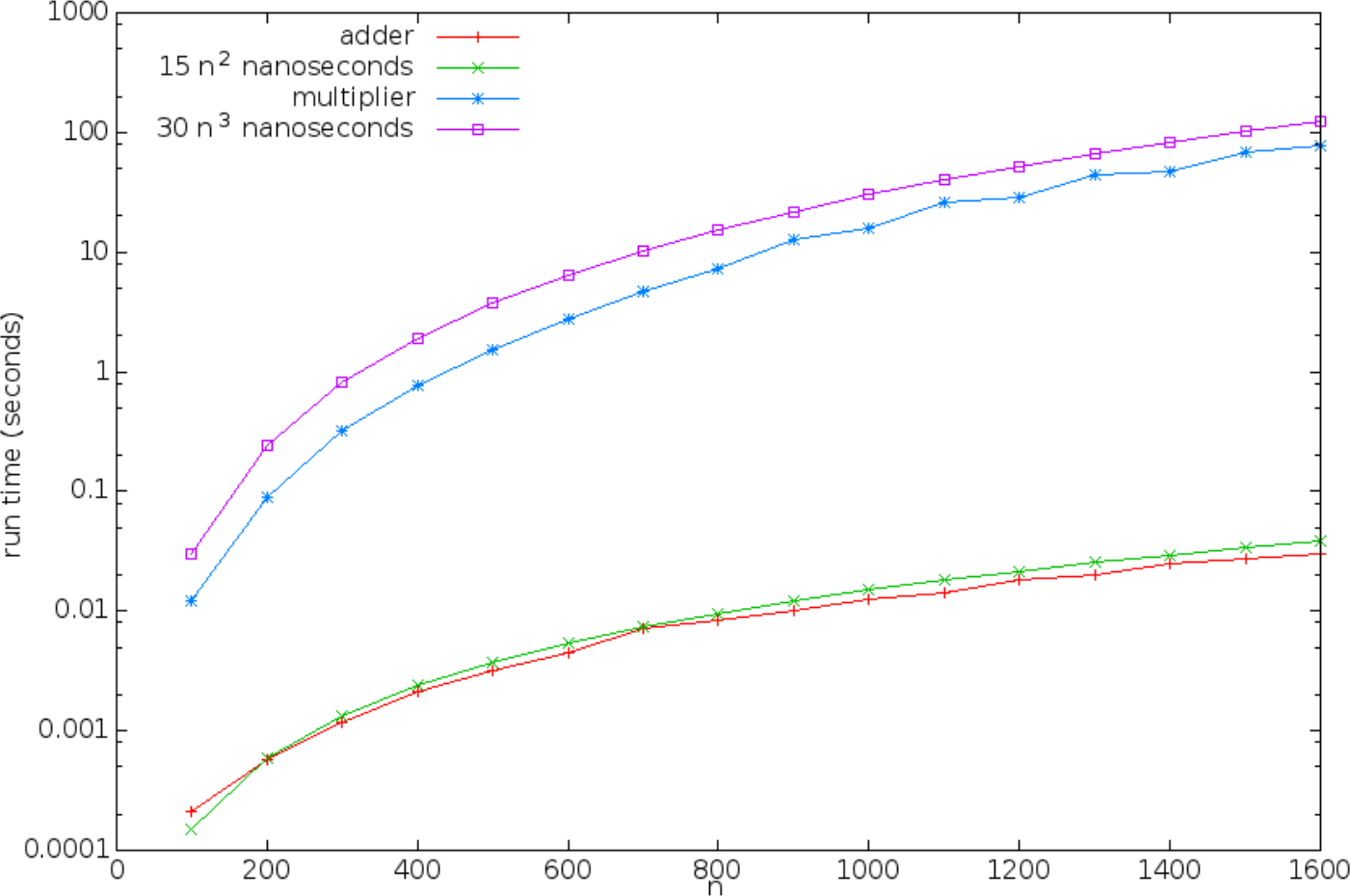
Profiling matrix operations run-time

Using measureCpuTimeRepeated, for matrix size \(n = 100, 200, \ldots, 1600\).

Fitting curves

• The previous running times were produced several years ago on a 3.1 GHz i5-2400 CPU with 8 GB RAM, and compiled using Scala 2.10.3.
  • They are far outdated now.
• The exact running times will vary with computer system, but

The shape of the curves will stay the same!

'Common' shapes

Big-O notation

• Actual running times are more complex than the basic functions we just saw
  • E.g. \(f\left(n\right) = 150n^3 + 2n^2 + 32\)
  • or \(f\left(n\right) = 44 n \log n + 15n\)
• The Big-O notation abstract away the constants and terms whose growth will be dominated by another term

• Definition (Big-O) ( "grows at most as fast as" ):

  For two (positive, real-valued) functions,\(f\) and \(g\), defined over non-negative integers \(n\) we write \(f(n) = \mathcal{O}(g(n))\) if there exist constants \(c,n_0 \gt 0\) such that \(f(n) \leq {c g(n)}\) for all \(n \geq n_0\).

• That is, \(f\) grows at most as \(g\) when \(n\) is large enough (up to a constant factor)

Comparing scaling using \(\mathcal{O}\)

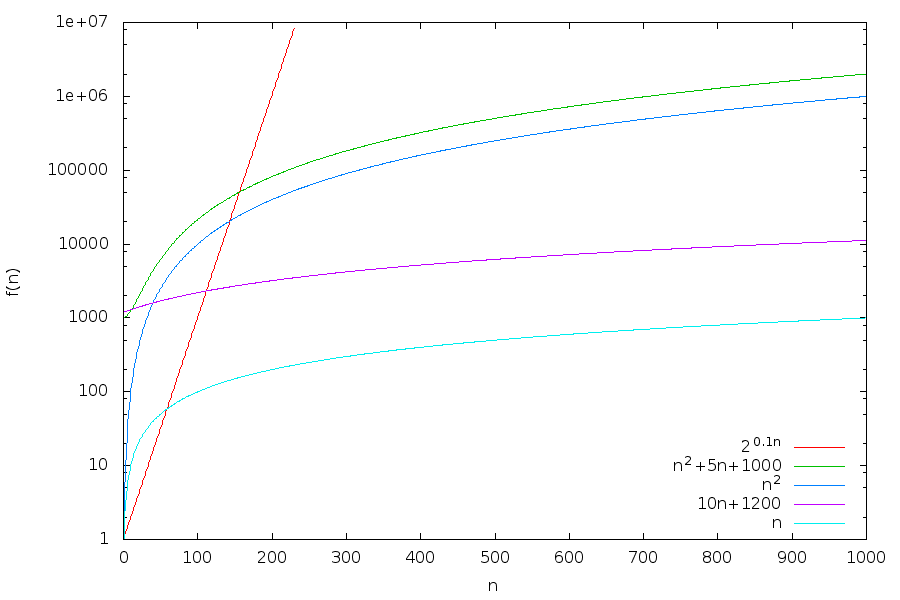
• \(n = \mathcal{O}\left(10n + 1200\right)\), by definition
• \(10n + 1200 = \mathcal{O}\left(n\right)\), because \(10n + 1200 \lt 12n\) when \(n > 600\)
• That is, \(10n + 1200\) and \(n\) are equivalent in the big-O notation

Comparing scaling using \(\mathcal{O}\)

• \(10n + 1200 = \mathcal{O}\left(n^2\right)\), because \(10n + 1200 \lt 10n^2\) when \(n > 12\) (It is actually little-o)
• \(n^2 \neq \mathcal{O}\left(10n + 1200\right)\), because \(\frac{n^2}{10n + 1200} \rightarrow \infty\) as \(n \rightarrow \infty\)
• \(n^2\) grows faster than \(10n + 1200\) in the big-O notation

Comparing scaling using \(\mathcal{O}\)

• Is \(n^2 + 5n + 1000 = \mathcal{O}(n^2) \)?
• What about \(n^2\)? Is it \(\mathcal{O}(n^2 + 5n + 1000)\)?
• What about \(2^{0.1n}\)? Is it \(\mathcal{O}(n^2)\)?

\(\Omega\) and \(\Theta\)

We can also define an upper bound (\(\Omega\)) and equality (\(\Theta\)) for scaling as

• Definition (\(\Omega\) - "grows at least as fast as" ):

  \( f\left(n\right) = \Omega\left(g\left(n\right)\right)\), if and only if \(g\left(n\right) = \mathcal{O}\left(f\left(n\right)\right)\)

• Definition (\(\Theta\) - "grows equally fast" ):

  \(f\left(n\right) = \Theta\left(g\left(n\right)\right)\), if and only if \(f\left(n\right) = \mathcal{O}\left(g\left(n\right)\right)\) and \(f\left(n\right) = \Omega\left(g\left(n\right)\right)\)

Big-O for running times

The running time for a function/method/program is \(\mathcal{O}\left(f\left(n\right)\right)\) if and only if for all inputs of size \(n\) the running time is \(\mathcal{O}\left(f\left(n\right)\right)\) time units.

Analysis based on code - matrix multiplication

/** Returns a new matrix that is the product of this and that */
def *(that: Matrix): Matrix =
    val result = new Matrix(n)
    for row <- 0 until n; column <- 0 until n do
        var v = 0.0
        for i <- 0 until n do
            v += this(row, i) * that(i, column)
        result(row, column) = v
    end for
    result
end *

We have to look at each statement and ask ourselves how many constant time instructions it takes.

Analysis based on code - matrix multiplication

/** Returns a new matrix that is the product of this and that */
def *(that: Matrix): Matrix =
    val result = new Matrix(n)                  // O(n^2)
    for row <- 0 until n; column <- 0 until n do
        var v = 0.0
        for i <- 0 until n do
            v += this(row, i) * that(i, column)
        result(row, column) = v
    end for
    result
end *

A Matrix contains \(n^2\) numbers - each needs to be initialised.

Analysis based on code - matrix multiplication

/** Returns a new matrix that is the product of this and that */
def *(that: Matrix): Matrix =
    val result = new Matrix(n)                  // O(n^2)
    for row <- 0 until n; column <- 0 until n do// O(n^2)
        var v = 0.0
        for i <- 0 until n do
            v += this(row, i) * that(i, column)
        result(row, column) = v
    end for
    result
end *

The for loop goes through all \(n^2\) elements.

Analysis based on code - matrix multiplication

/** Returns a new matrix that is the product of this and that */
def *(that: Matrix): Matrix =
    val result = new Matrix(n)                  // O(n^2)
    for row <- 0 until n; column <- 0 until n do// O(n^2)
        var v = 0.0                             // O(n^2)
        for i <- 0 until n do
            v += this(row, i) * that(i, column)
        result(row, column) = v
    end for
    result
end *

Assignment is \(\mathcal{O}(1)\), but applied \(\mathcal{O}(n^2)\) times due to loop.

Analysis based on code - matrix multiplication

/** Returns a new matrix that is the product of this and that */
def *(that: Matrix): Matrix =
    val result = new Matrix(n)                  // O(n^2)
    for row <- 0 until n; column <- 0 until n do// O(n^2)
        var v = 0.0                             // O(n^2)
        for i <- 0 until n do                   // O(n^3)
            v += this(row, i) * that(i, column)
        result(row, column) = v
    end for
    result
end *

Loop by itself is \(\mathcal{O}(n)\), but inside \(\mathcal{O}(n^2)\) loop, so \(\mathcal{O}(n^3)\).

Analysis based on code - matrix multiplication

/** Returns a new matrix that is the product of this and that */
def *(that: Matrix): Matrix =
    val result = new Matrix(n)                  // O(n^2)
    for row <- 0 until n; column <- 0 until n do// O(n^2)
        var v = 0.0                             // O(n^2)
        for i <- 0 until n do                   // O(n^3)
            v += this(row, i) * that(i, column) // O(n^3)
        result(row, column) = v
    end for
    result
end *

Several constant time operations inside loop. Important: Why are accessing values constant in this case?

Analysis based on code - matrix multiplication

/** Returns a new matrix that is the product of this and that */
def *(that: Matrix): Matrix =
    val result = new Matrix(n)                  // O(n^2)
    for row <- 0 until n; column <- 0 until n do// O(n^2)
        var v = 0.0                             // O(n^2)
        for i <- 0 until n do                   // O(n^3)
            v += this(row, i) * that(i, column) // O(n^3)
        result(row, column) = v                 // O(n^2)
    end for
    result
end *

Performed \(\mathcal{O}(n^2)\) times. Again - assumes assignment of value to element is \(\mathcal{O}(1)\).

Analysis based on code - matrix multiplication

/** Returns a new matrix that is the product of this and that */
def *(that: Matrix): Matrix =
    val result = new Matrix(n)                  // O(n^2)
    for row <- 0 until n; column <- 0 until n do// O(n^2)
        var v = 0.0                             // O(n^2)
        for i <- 0 until n do                   // O(n^3)
            v += this(row, i) * that(i, column) // O(n^3)
        result(row, column) = v                 // O(n^2)
    end for
    result                                      // O(1)
end *

Analysis based on code - rules of thumb

• Nested loops over data increases one polynomial order
• Method/function calls can hide complexity
• Data structures matters!
  • E.g. if we use Array or List to represent the matrix elements
• Therefore, always make sure you know what data structure is used
• Always document performance characteristics when you provide a library/package
  • (Like Scala does for collections)

Optimising the constant factor

• big-O ignores constant factors
• Scaling of algorithms and data structures is extremely important for efficient code
• But in practice, optimising the constant factor can lead to large savings in time (and energy)
• Example in the course notes optimising Matrix multiplication

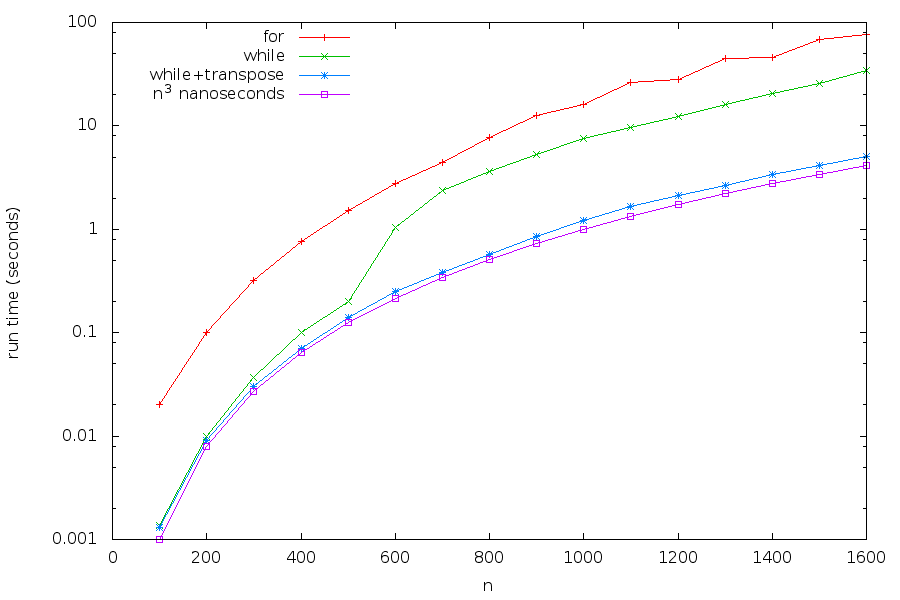
Almost 30-fold increase! - But still \(\mathcal{O}(n^3)\)

(Code optimisation of constant factors means less readability - only optimise when necessary)

Searching - a common problem

• Finding an element in a collection is a very common problem
• Involves going over the elements in a collection until
  • the element is found, or
  • we know it isn't there
• As searching is very common the efficiency is important

Disorder and linear search

• If the collection is disordered (or we know nothing about it), then essentially the best we can do is Linear search
  • E.g. Look for 19 in (4,24,7,11,4,7,21,23,8,19,1,30)
  • Go through the collection start to finish until the element is found or we have reached the end

def linearSearch[T](s: IndexedSeq[T], k: T): Boolean =
  var i = 0
  while(i < s.length)  do
    if(s(i) == k) then return true // found k at position i
    i = i + 1
  end while
  false // no k in sequence
end linearSearch

• Assuming testing for equality and indexed access (s(i)) are constant time, linear search is \(\mathcal{O}(n)\).
• Not bad, but very often code search the same collection many times repeatedly ⇒ that code is \(\mathcal{O}(n^2)\)
  • One n from the repeated search times the n from the search itself.

Indexing - imposing structure

• If we know that a collection will be searched repeatedly it could pay off to analyse it first
• This process is generally known as indexing
• The most common form of indexing is sorting
  • (Requires that we have some idea about how to order the elements in some sense)
• Index is created once, so if that cost is not prohibitive, and it is effective to use this could pay off

Order and binary search

• Assume instead that we have a collection of perfectly ordered data
  • E.g. look for 19 in (1,4,4,7,7,8,11,19,21,23,24,30)
• Will this structure allow us to do better than linear search?
• Yes - binary search:
  • Suppose we need to find the element k in sequence s
  • Assume s is already sorted in ascending order
  • If s is empty the element cannot be found. Stop.
  • Let m be the middle (rounded down) element of s:
    • if k = m, we are done. Stop.
    • if k < m, then the key can only appear in the first half of the sequence
      • Recursively search over on the first half of s only
    • if k > m, then the key can only appear in the second half of the sequence
      • Recursively search over on the second half of s only

Binary search - example

Binary search in Scala

def binarySearch[T](s: IndexedSeq[T], k: T)(using Ordering[T]) : Boolean =
  import math.Ordered.orderingToOrdered // To use the given Ordering
  //require(s.sliding(2).forall(p => p(0) <= p(1)), "s should be sorted")
  def inner(start: Int, end: Int): Int =
    if !(start < end) then start
    else
      val mid = (start + end) / 2
      val cmp = k compare s(mid)
      if cmp == 0 then mid                     // k == s(mid)
      else if cmp < 0 then inner(start, mid-1) // k < s(mid)
      else inner(mid+1, end)                   // k > s(mid)
    end if
  end inner
  if s.length == 0 then false
  else s(inner(0, s.length-1)) == k
end binarySearch

Efficiency of binary search

• Again, assuming comparisons (=, <, >) and access takes constant time
• Each 'step' of the binary search algorithm only contains \(\mathcal{O}(1)\) operations
• But, it is called recursively
• What is the maximum number of times it is called?
  • Stops when element is found, or called on zero length sequence
  • Each recursive call the length of the sequence is halved
• If the original sequence length is \(n\), then the recursive calls are on lengths are on lengths \(\frac{n}{2^1},\frac{n}{2^2},\ldots\)
  • until some \(\left\lfloor\frac{n}{2^k}\right\rfloor = 0\)
  • That is in \(k = \log n\) recursive calls
• So binary search is \(\mathcal{O}(\log n)\)

Sorting + Binary search efficiency

• When the sequence is ordered search can be done in \(\mathcal{O}(\log n)\)
• Great, but what is the cost of sorting?
  • Comparison-based sorting algorithms (Scala's sorted method) work in time \(\mathcal{O}(n \log n)\)
• ⇒ efficiency of sort + search is \(\mathcal{O}(n \log n) + \mathcal{O}(\log n) = \mathcal{O}(n \log n)\)
• This is worse than linear search, \(\mathcal{O}(n)\)!
  • Yes, but we only sort once!
• So, say you are doing \(n\) repeated searches, then effectively
  • Binary search: \(\mathcal{O}(n \log n) + \mathcal{O}(n) \times \mathcal{O}(\log n) = \mathcal{O}(n \log n)\)
  • Linear search: \(\mathcal{O}(n) \times \mathcal{O}(n) = \mathcal{O}(n^2)\)
• Rule of thumb: Only a handful of searches - it may not be worth processing the data, if the number of searches is large indexing pays off

But, does it matter?

• Yes!
  • In practice, e.g
    • huge data sets ⇒ huge \(n\)
    • millions of users ⇒ app is run millions of times
    • energy consumption* ⇐ computing generally require energy (Landauer's principle)
  • In theory
    • Computational complexity - the study of how hard problems are and what we fundamentally can compute

Comparing run times: Assuming unit of \(f(n)\) to 1 ns. Here d denotes days, a denotes years.

Exercises