Indexing and search
Everyday experience hints that if we get to choose between disorder and order, from the perspective of efficiency it may be serendipitous to choose order.
Indeed, look at the two sequences of characters below:
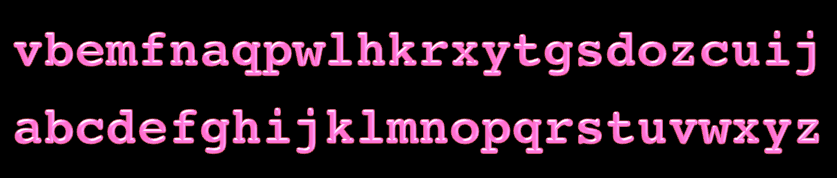
Both sequences contain the same characters.
The first sequence is arguably disordered (or unstructured), whereas the second sequence is arguably more ordered (or structured).
Disorder and order, searching
Suppose we now need to search a sequence of characters
for a particular character, say, the character “x”:
Does the character occur in the sequence?
If so, how many times, and in what precise positions?
Again everyday experience suggests that order enables a more efficient search than disorder.
Let us, however, start with disorder.
Linear search
Suppose we are faced with an indexed sequence of elements of some type T.
Suppose furthermore that we know absolutely nothing about the sequence.
For all we know, there is no structure whatsoever in the sequence.
How efficiently can we search such a sequence for a particular element
(or key) of type T ?
One possibility is just to perform a linear search, that is,
we iterate through the sequence, one element at a time,
and see whether we can find the key k:
def linearSearch[T](s: IndexedSeq[T], k: T): Boolean =
var i = 0
while(i < s.length) do
if(s(i) == k) then return true // found k at position i
i = i + 1
end while
false // no k in sequence
end linearSearch
From the perspective of efficiency, if
testing elements for equality, and
indexed access to elements of the sequence
are both constant-time operations, then linear search takes \(\mathcal{O}(n)\) time for a sequence of length \(n\).
What is more, if we really know absolutely nothing about the sequence,
then linear search is essentially the best we can do.
That is, in the worst case we must access every element and test it
for equality against the key k. Indeed, any element left unaccessed
or untested could have been the only element that is equal to the key,
so every element must be accessed and tested.
Note
The scala.collection classes that integrate the scala.collection.Seq trait use linear search to implement
the method find through the
scala.collection.Iterator trait
Warning
Despite its name, linear search may take more than linear time if
it is not a constant-time operation to test two values of type T
for equality. This is the case, for example, if the values are
long strings or other complicated objects that may require
substantial effort to test for equality.
Indexing and sorting
While linear search is the best we can do to search unstructured or unknown data, of course there is nothing that forces the data to remain unstructured once we have access to it.
Indeed, as soon as we have access, we should invest resources to introduce structure to the data to enable fast search. Once we know that the data has a particular structure, we can take advantage of this structure when we search the data.
Note
Such an approach of investing resources to introduce structure to enable subsequent fast search is called indexing the data.
Perhaps the most common form of indexing is that we sort the data so that the keys appear in increasing (or decreasing) order. Once we know that this is the case, then we can take advantage of the order when we search the data.
Binary search
Suppose we have a sequence \(s\) of elements that has been sorted to increasing order. Now suppose we must search whether a key \(k\) occurs in \(s\).
Consider the middle element \(m\) in \(s\). We observe the following three cases:
If \(k = m\), we have found the key \(k\) so we can stop immediately.
If \(k < m\), then the key \(k\) can appear only in the first half of the sequence.
If \(k > m\), then the key \(k\) can appear only in the second half of the sequence.
In the latter two cases, we recursively continue in the selected half of the sequence until either
we find the key \(k\), or
the subsequence under consideration is empty, in which case we conclude that the key \(k\) does not appear in \(s\).
For example, below we display the steps of
binary search for the key 19 in the ordered sequence
[1,4,4,7,7,8,11,19,21,23,24,30]. In each step, we highlight
with blue the current subsequence defined by the indices start and end:
That is, in the first step we start with the entire sequence and consider
its middle element 8 (let us agree that when the sequence has even length,
the middle element is the leftmost of the two available choices for
the middle element). As the sequence is sorted and 8 is less than the key 19,
we conclude that 19 can occur only in the second half of the sequence,
not including the middle element 8. We then repeat the same with the
subsequence consisting of the second half. Its middle element is 21,
which is greater than the key 19.
We thus next consider the first half of this subsequence,
whose middle element is 11. In the last step the subsequence consists
of one element, and this element is both the middle element and
is equal to the key 19. Thus we have discovered 19 in the sequence.
Observe that only the 4 elements (8, 21, 11 and 19) indexed by the middle
point index mid in the figure are compared against the key 19.
As a second example, let us search for the key 6 in the same sorted sequence:
In the last step, there are no more elements to consider in the subsequence and we conclude that 6 does not appear in the sequence.
Implementing binary search in Scala
Now that we understand how binary search operates, let us implement it in Scala.
First, we must make sure that our sequence is sorted and supports
constant-time indexed access to its elements. If this is not the case,
we prepare a sorted copy of the sequence with the sorted method
and then (if necessary) transform the sorted collection into a type
that supports constant-time indexed access, for example, by calling its
toIndexedSeq (or toArray or toVector) method.
As we are not modifying the sequence during search,
we need not create new sequence objects for the considered
subsequences but can simply track the start and end of the
current subsequence with two indices (start and end).
We can now implement binary search as a recursive function:
def binarySearch[T](s: IndexedSeq[T], k: T)(using Ordering[T]) : Boolean =
import math.Ordered.orderingToOrdered // To use the given Ordering
//require(s.sliding(2).forall(p => p(0) <= p(1)), "s should be sorted")
def inner(start: Int, end: Int): Int =
if !(start < end) then start
else
val mid = (start + end) / 2
val cmp = k compare s(mid)
if cmp == 0 then mid // k == s(mid)
else if cmp < 0 then inner(start, mid-1) // k < s(mid)
else inner(mid+1, end) // k > s(mid)
end if
end inner
if s.length == 0 then false
else s(inner(0, s.length-1)) == k
end binarySearch
Let us test the function with some sample inputs:
scala> val s = Vector(1,4,4,7,7,8,11,19,21,23,24,30)
s: scala.collection.immutable.Vector[Int] = Vector(1, 4, 4, 7, 7, 8, 11, 19, 21, 23, 24, 30)
scala> binarySearch(s, 19)
res: Boolean = true
scala> binarySearch(s, 6)
res: Boolean = false
Observe that the recursion takes place in the inner function inner because
the recursive calls have to know the start and end of the current
subsequence, and these parameters are not available in the outer function
binarySearch. Also, the first require statement is not included but
rather is commented out because its evaluation is (for long sequences)
substantially slower than the rest of the function.
One can include it, for instance, in the testing phase of a larger project
so that illegal calls to the function with non-sorted sequences can be caught.
For a sorted sequence with \(n\) elements
with constant-time indexed access and compare operator,
the run-time of binarySearch is in \(\mathcal{O}(\log n)\):
The number of elements under consideration,
end - start + 1, at least halves in each recursive callWe stop when
start >= end(that is, whenend - start + 1 <= 1)How many halvings suffice until we have decreased the original \(n\)-element sequence into a one-element sequence? Denoting the number of halvings by \(h\), we have \(n/2^h \le 1\), which implies \(n \le 2^h\) and thus \(h \ge \log n\).
Under the previous assumptions, each halving takes constant time and thus the run-time is \(\mathcal{O}(\log n)\).
The number of calls to the compare operator is
\(\mathcal{O}(\log n)\). This matters in particular if comparison is
an expensive operation, for example, when the elements are long strings
or other more complicated objects.
We have thus established that compared with linear search, binary search is a very fast way to search for a key in a sorted sequence.
If the sequence is initially not sorted but we have to sort it first
to enable binary search, then we should include the time to sort
into the analysis. The most efficient general purpose
comparison-based sorting algorithms, such as the sorting algorithm that is implemented in
the sorted method, work in time \(\mathcal{O}(n \log n)\).
(Here we again assume comparisons are constant-time operations.)
Now, if the sequence is initially unstructured and we make only
one search after the sequence is sorted, the total run-time will be
\(\mathcal{O}(n \log n) + \mathcal{O}(\log n) = \mathcal{O}(n \log n)\),
which is in total slower than just running linear search on the
unstructured input without sorting. On the other hand, if we make
a large number of searches to the sequence then it pays off to first
sort and then run binary search. Similarly, if we can afford to invest
time to preprocess our input before any searches take place, and each
search needs to be executed as fast as possible (for example, to supply a smooth
and responsive user experience), then it again pays off to use binary search.
Note
Although binary search is conceptually quite straightforward, its implementations are surprisingly prone to subtle errors.
Note
The declaration implicit ev: T=>Ordered[T] in the function says that
the class T of the elements in the sequence s must be such
that it can be converted to an Ordered[T] class
which provides the compare method used in the function. Moreover that a function ev (evidence) should be provided implicitly by Scala if such a conversion exists, so that the function can be called as binarySearch(s,k).
Note
Recursion is a natural way to implement binary search but we can also make an iterative implementation:
def binarySearchIter[T](s: IndexedSeq[T], k: T)(using Ordering[T]): Boolean =
import math.Ordered.orderingToOrdered // To use the given Ordering
//require(s.sliding(2).forall(p => p(0) <= p(1)), "s should be sorted")
if s.length == 0 then return false
var start = 0
var end = s.length - 1
while(start < end) do
val mid = (start + end) / 2
val cmp = k compare s(mid)
if cmp == 0 then {start = mid; end = mid}
else if cmp < 0 then end = mid-1 // k < s(mid)
else start = mid+1 // k > s(mid)
end while
return s(start) == k
end binarySearchIter