Programming the armlet
All right, that was a lengthy description of how the machine operates and how it is designed. Now it is time to get back to programming and convince ourselves that the machine actually is programmable.
Our first armlet program
Here is our first program for the armlet. As you can
observe, the program is not written in binary:
# Stores into $2 the sum of the first $0 positive integers
mov $0, 10 # initially 10 summands remain
mov $1, 1 # positive integers start from 1
mov $2, 0 # the sum starts at 0
@loop:
cmp $0, 0 # compare number of summands remaining with zero
beq >done # ... branch to label @done if zero summands remain
add $2, $2, $1 # add the current integer to the sum
add $1, $1, 1 # update the current integer to next
sub $0, $0, 1 # decrease number of integers to sum
jmp >loop # jump to label @loop
@done:
hlt # halt the processor
Of course, our poor armlet has no idea about the program text
above. There is only so far 5574 gates can be pushed in terms
of reading comprehension.
However, the armlet has been purpose-built with extreme
care to understand the following sequence of 16-bit words, stored in
the memory unit, starting from address 00000:
00000: 0000000000011010
00001: 0000000000001010
00002: 0000000001011010
00003: 0000000000000001
00004: 0000000010011010
00005: 0000000000000000
00006: 0000000000100011
00007: 0000000000000000
00008: 0000000000100101
00009: 0000000000010001
00010: 0001010010000110
00011: 0000001001011110
00012: 0000000000000001
00013: 0000000000011111
00014: 0000000000000001
00015: 0000000000100100
00016: 0000000000000110
00017: 0000000000111111
Indeed, after exactly 120 clock ticks, the armlet halts
with the value \(55 = 1 + 2 + \ldots + 10\) in $2.
Assembly language
In the early days of computing it used to be the case that coding meant actually the act of toggling in the program to a memory unit, in binary (or other) code, using physical switches or other physical means to interact with the memory unit. (See here.) Fortunately, these days are past.
The program text above is written in the armlet
assembly language, which is a symbolic,
human-readable, and human-comment-decorated representation of the
binary code, with minor convenience features. One of the convenience
features is the possibility to use symbolic labels such as “@done”
and “@loop” to label addresses in the eventual binary, and
the possibility to refer to these addresses using symbolic references
such as “>done” and “>loop”.
The assembler
Once the program text is ready, it is then the responsibility of a
program, the armlet assembler to automatically
turn, or assemble, the decorated assembly-language program text
into the binary code that the armlet understands if it is loaded
(in precise terms, stored) into the memory unit.
Again our pedagogical guideline is to hide nothing, so we observe
that the armlet assembler is less than 300 lines of Scala code
and is part of package armlet.
The input to the assembler is a string of program text and the output
is a sequence of binary words that will put the armlet to work
if we so choose.
A playful introduction to Ticker
It is about time for a bit of play. And now that the armlet is ready,
perhaps it is time to improve our play beyond toggling.
Towards this end, we are pleased to introduce Ticker,
a complete interactive program to play with the armlet architecture,
either one clock tick at a time, or (one expects) at least at
a few thousand simulated clock ticks per second.
Copy and paste the following into a console:
import armlet._ // Packages in |round-pfx:sequential-logic| and |round-pfx:a-programmable-computer|
new Ticker()
A Ticker interface should pop up. The top left text area accepts
program text in armlet assembly language.
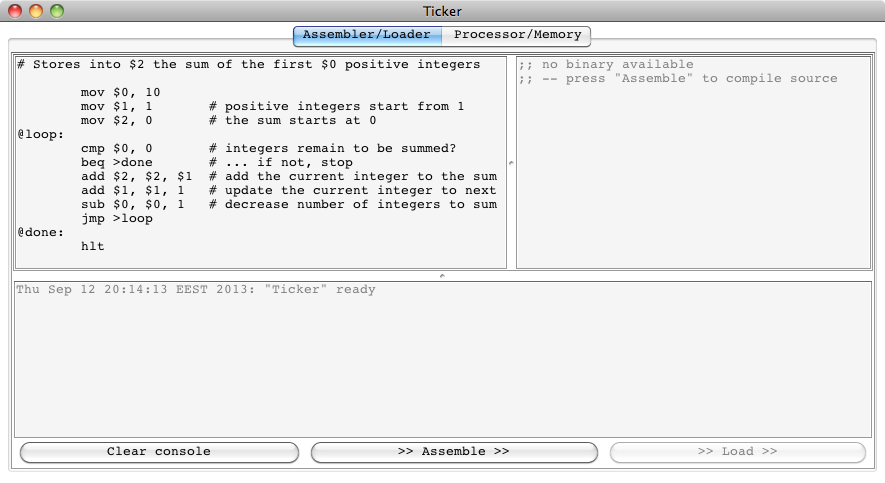
So let us type in some program text, that is, our first armlet
program above:
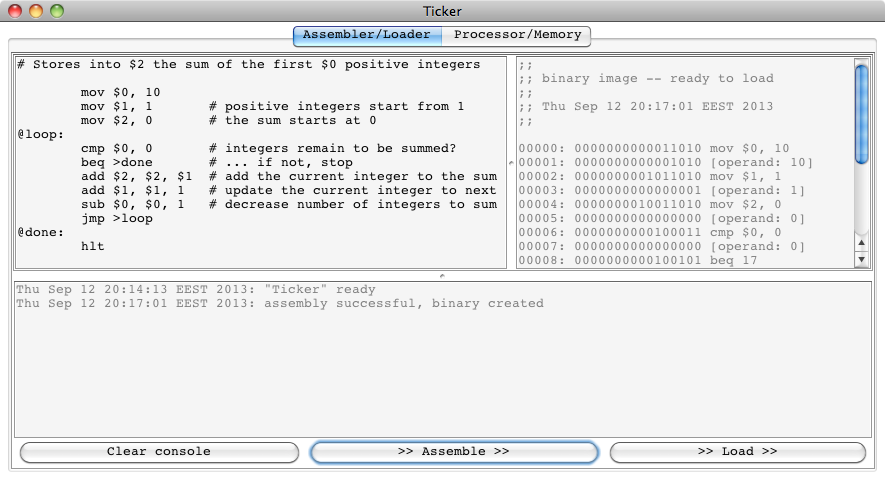
We can now click “>> Assemble >>” to turn the program text
into a binary.
And indeed the binary appears in the loader window on the top right:
If we click “>> Load >>”, the binary is loaded into the
memory unit and the armlet is reset.
We are ready to tick or run:
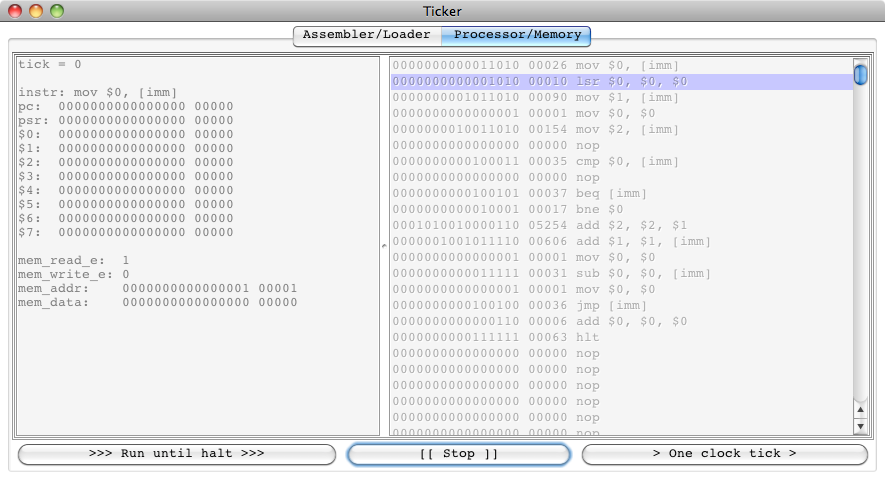
If we choose to run, we get a halt at tick 120:
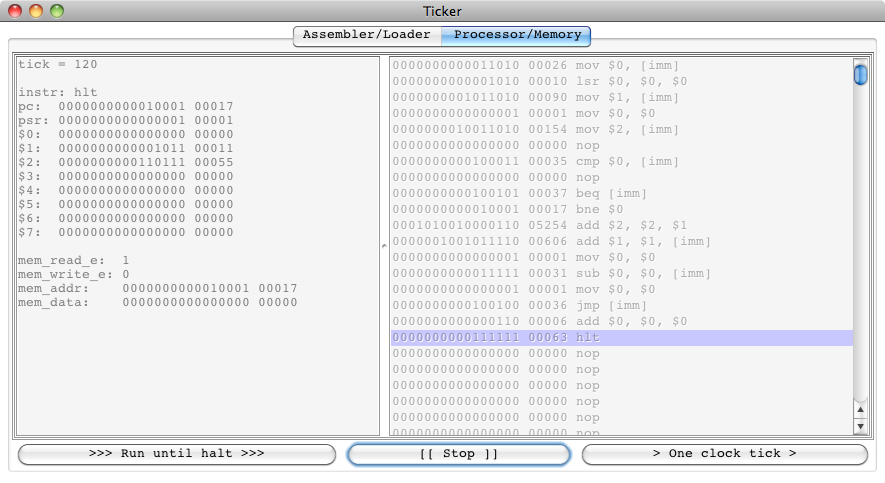
Pressing “[[ Stop ]]” will bring back the Assembler/Loader
view. Incidentally, you can change between views by clicking on the
titles “Assembler/Loader” and “Processor/Memory”.
You are now cordially invited to play with the armlet.
Watch the processor obediently execute whatever you want, with full
view of what happens, one tick at a time, or at a few kHz until halt.
Beyond the first example
Let us now practice programming the armlet a little bit to gain
confidence that the design is fully programmable and not just a useless
toy. Indeed, even if the armlet may appear like a humble design,
it is in fact equally capable as any computer, and only restricted by
the limitations of the 16-bit design and the \(2^{16} = 65536\) words
of memory it can address. With wider word length to enable the processor
to address more memory, the armlet could simulate any modern
computer. (See
here
for a more detailed discussion.)
Let us now look at a few examples how to program the armlet.
Again we start simple and get more ambitious gradually.
Scanning data
Computers are used to process information, so it is perhaps natural to start with code that searches and indexes numeric data.
To prepare a numeric array for input to the armlet, we
can declare it in the assembly language as follows:
# Here is my data, which consists of 20 words:
@my_data:
%data 296, 573, 291, 415, 825, 674, 426, 632, 793, 701, 884, 1, 989, 912, 254, 869, 462, 296, 767, 220
In other words, we have a label “my_data” for the memory address
that contains the data, which is a sequence of (20) words that we declare with
the %data keyword.
We should also record the length of the data so that our eventual program will know how many words of data it has to process:
# Here is my data:
@length_of_my_data:
%data 20
@my_data:
%data 296, 573, 291, 415, 825, 674, 426, 632, 793, 701, 884, 1, 989, 912, 254, 869, 462, 296, 767, 220
The declarations above will now cause the assembler to include 21 words of
data into the compiled (assembled) binary. The loader will then load the
data to the armlet for whatever processing we like.
So let us get started with something simple. Let us compute the sum
of the data in $0 and then halt the processor.
Here we go:
# Computes (to $0) the sum of the data and then halts.
# Let us first set things up ...
mov $0, 0 # the sum starts with 0
mov $2, >length_of_my_data # set up memory address where to get length
loa $2, $2 # load the length from memory to $2
mov $1, >my_data # set up memory address where to get the data
# Now let us loop through the data and accumulate the sum ...
@sum_loop:
cmp $2, 0 # compare length with 0
beq >done # ... branch to label @done if $2 == 0
loa $3, $1 # load a data item from memory
add $0, $0, $3 # accumulate the sum in $0
add $1, $1, 1 # advance to next data item
sub $2, $2, 1 # decrement length by one
jmp >sum_loop # continue the summation
# ... until we are done
@done:
hlt # the processor stops here
# Our data follows the program code in the binary ...
# Here is my data:
@length_of_my_data:
%data 20
@my_data:
%data 296, 573, 291, 415, 825, 674, 426, 632, 793, 701, 884, 1, 989, 912, 254, 869, 462, 296, 767, 220
Using Ticker we find that the processor halts at tick 272, at
which point we find 11280 in $0. Thus, we find that the armlet
has no problem with simple processing of numeric data.
So let us get a little more ambitious. Say, let us find the maximum value in the data:
# Finds the maximum value ($0) and its position ($1) in data and then halts.
# Let us first set things up ...
mov $3, >length_of_my_data # set up memory address where to get length
loa $3, $3 # load the length from memory to $3
mov $2, >my_data # set up memory address where to get the data
cmp $3, 0 # compare length with 0
bab >have_data # ... if length > 0, branch to process data
hlt # ... otherwise halt immediately
@have_data:
mov $4, $2 # set up first address
add $5, $4, $3 # set up last address
loa $0, $4 # set up a candidate maximum
sub $1, $4, $2 # set up position of candidate maximum
add $4, $4, 1 # advance current address
cmp $4, $5 # are we at the last address?
bbw >max_scan_loop # ... if not, continue scanning
jmp >done # ... otherwise we are done
# ... and then scan for the maximum, updating the candidate maximum
@max_scan_loop:
loa $6, $4 # load current data item
cmp $6, $0 # compare current with candidate maximum
bbe >no_update # ... if current <= candidate, no update
mov $0, $6 # ... update candidate maximum
sub $1, $4, $2 # ... and its position
@no_update:
add $4, $4, 1 # advance current address
cmp $4, $5 # compare current address with last address
bbw >max_scan_loop # ... if curr addr < last addr, continue scan
# ... until we are done
@done:
hlt # the processor stops here
# Our data follows the program code in the binary ...
# Here is my data:
@length_of_my_data:
%data 20
@my_data:
%data 296, 573, 291, 415, 825, 674, 426, 632, 793, 701, 884, 1, 989, 912, 254, 869, 462, 296, 767, 220
Executing the code above, a halt occurs at tick 218, at which point we
find 989 in $0 and 12 in $1. It would thus appear that
the armlet is perfectly able to do minor tasks. We also observe
that the structure of the code has an effect on performance. In particular,
the simple summation took 272 ticks, whereas the maximum-finding took
only 218 ticks by a slightly more careful use of the registers and
structuring of the loops.
An important lesson to be learned while programming the armlet
in assembly language is that it is not particularly pleasant to program
in assembly language from the programmer’s perspective. Indeed, the machine
will do exactly what we tell it to do, but there are few conveniences
available. The programmer must mentally keep track of what is in the
registers at any given point of execution and must access memory with
explicit addresses. A much greater level of programmer productivity and
program portability is achieved by using a high-level programming language
such as Scala, even if program performance may, and in general is, lost
in terms of increased running time or increased memory usage.
Yet an important fact to keep in mind is that all high-level programming
tools are simply convenience tools to assist the programmer. At heart,
every modern computer processor is, from a qualitative perspective, not
substantially different from the armlet. Even the Scala programming
language is just a convenience tool for translating the programmer’s
high-level instructions for execution on physical hardware.
Sorting data
Scanning through the data may not appear that impressive, so let us turn to
a somewhat more challenging task, sorting. In particular, with the
armlet we have neither convenience tools nor existing code available
to help us with sorting, so we must implement everything ourselves,
from scratch.
There are a myriad of different strategies to sort data. Since we already know how to scan data for the maximum element, perhaps the sorting strategy that is easiest to implement is to repeatedly find the maximum element in the current array, transpose the maximum element with the last element in the current array, and disregard the last element of the current array from consideration. The data is sorted when the current array is empty. This strategy is called selection sort since we repeatedly select the maximum element.
Here is an implementation of selection sort for the armlet:
# Selection sort for the armlet
mov $0, >data # set up start address
mov $1, >datalen # set up address where to get length
loa $1, $1 # load length
add $1, $1, $0
sub $1, $1, 1 # address of the last data item
@select_loop:
cmp $0, $1 # compare start address and last address
bae >done # ... if start addr >= last addr, we are done
loa $2, $0 # set up a candidate maximum
mov $3, $0 # set up address of candidate maximum
add $4, $0, 1 # set up current address
@max_scan_loop:
cmp $4, $1 # compare current address with last address
bab >scan_done # ... if curr addr > last addr, we have the max
loa $5, $4 # load current data item
cmp $5, $2 # compare current item with candidate max
bbe >no_update # ... if current <= candidate, no need to update
mov $2, $5 # update candidate maximum
mov $3, $4 # update address of candidate maximum
@no_update:
add $4, $4, 1 # advance to next element
jmp >max_scan_loop # continue scanning
@scan_done:
# at this point $2 is the max item and $3 is its addr in array
# transpose max item and last item in current array ...
sub $4, $4, 1 # address of last item
loa $5, $4 # load last item
sto $4, $2 # store max to last position
sto $3, $5 # store last item to max position
sub $1, $1, 1 # remove last item (now =max) from consideration
jmp >select_loop # continue sorting the remaining array
@done:
hlt
@datalen:
%data 100
@data:
%randperm 1234567, 100
Observe the assembler directive %randperm 1234567, 100.
This is a convenience tool in the assembler to produce a random permutation
of the integers \(1, 2, \ldots, 100\) using the random seed 1234567 to
seed the Scala pseudorandom generator.
That is to say, the assembler will create the pseudorandom permutation
that is then included in the binary.
The program halts at tick 62305, having sorted the random permutation
into the sorted order \(1, 2, \ldots, 100\).
(Do check this with the memory view in Ticker!)
But that was only 100 integers. Hardly something to write home about.
Let us really push the armlet now. How about a permutation with,
say, 30000 integers? (Remember that the armlet has only 65536 words of
memory!)
Incidentally, selection sorting is not a good idea, since using selection sort we need to scan 30000 times for the maximum, and scan number \(j = 1, 2, \ldots, 30000\) requires us to iterate over \(30000 - j\) entries, implying that no matter what, selection-sorting 30000 words will thus require about 450 million ticks, and in fact many more. This will take a macroscopic amount of time even if executed on a serious computer.
Below is an implementation of a different sorting strategy, namely a heap sort, which will be studied in more detail later in the context of algorithms and data structures. For now, all we need to observe is that the code looks to be doing what appears to be something more serious:
# Heap sort for the armlet
mov $6, >datalen
loa $6, $6
mov $7, >data
sub $7, $7, 1 # index origin is 1
mov $0, 1 # start heapifying at the origin
@heapify:
cmp $0, $6 # done with heapify?
bab >getmax # ... yes
mov $1, $0 # current index
add $3, $7, $1 # address of current
loa $2, $3 # load current value
@upheap_loop:
cmp $1, 1 # at heap top?
bbe >heapify_next # ... yes
lsr $3, $1, 1 # index of parent
add $4, $7, $3 # address of parent
loa $4, $4 # load parent
cmp $4, $2 # compare parent and current
bae >heapify_next # ... heap property holds
add $5, $7, $1 # address of current
sto $5, $4 # store parent to current
mov $1, $3 # move to parent
jmp >upheap_loop
@heapify_next:
add $3, $7, $1 # address of current
sto $3, $2 # store current value here
add $0, $0, 1
jmp >heapify
@getmax:
cmp $6, 0 # done with max extraction?
beq >done # yes
add $0, $7, 1 # address of heap top
loa $3, $0 # load heap top
add $2, $7, $6 # address of last element
loa $1, $2 # load last element
sto $2, $3 # heap top goes to last element
sub $6, $6, 1 # decrease heap size
mov $0, 1 # start downheap, $1 is current
@downheap_loop:
lsl $2, $0, 1 # left child index
cmp $2, $6 # is there a left child?
bab >downheap_done # ... no
add $4, $2, $7 # left child address
loa $4, $4 # load left child
add $3, $2, 1 # right child index
cmp $3, $6 # is there a right child?
bab >downheap_left # ... no
add $5, $3, $7 # right child address
loa $5, $5 # load right child
cmp $4, $5 # compare children
bae >downheap_left # ... go left
@downheap_right:
cmp $1, $5 # compare current and right
bae >downheap_done # ... ok to insert at current
add $2, $7, $0 # current address
sto $2, $5 # insert right to current
mov $0, $3 # move to right
jmp >downheap_loop
@downheap_left:
cmp $1, $4 # compare current and left
bae >downheap_done # ... ok to insert at current
add $3, $7, $0 # current address
sto $3, $4 # insert left to current
mov $0, $2 # move to left
jmp >downheap_loop
@downheap_done:
add $2, $7, $0 # current address
sto $2, $1 # store current here
jmp >getmax
@done:
hlt
@datalen:
%data 30000
@data:
%randperm 1234567, 30000
In the last line above we observe a random permutation with 30000 elements.
It will take some time for the armlet to finish the sort, in fact
a halt will occur at tick 12647480, or in about 13 million ticks for this
particular random permutation.
At this point it should be immediate that the armlet with
its 5574 gates is able to do serious work if we are serious about programming
it. The exercises will present some further challenges in this regard.
Some conventions and hints for the exercises
(You can download a quick-reference for armlet here)
Let us first summarize the armlet instruction set.
Here are the arithmetic and logic instructions that operate on registers:
nop # no operation
mov $L, $A # $L = $A (copy the value of $A to $L)
and $L, $A, $B # $L = bitwise AND of $A and $B
ior $L, $A, $B # $L = bitwise (inclusive) OR of $A and $B
eor $L, $A, $B # $L = bitwise exclusive-OR of $A and $B
not $L, $A # $L = bitwise NOT of $A
add $L, $A, $B # $L = $A + $B
sub $L, $A, $B # $L = $A - $B
neg $L, $A # $L = -$A
lsl $L, $A, $B # $L = $A shifted to the left by $B bits
lsr $L, $A, $B # $L = $A shifted to the right by $B bits
asr $L, $A, $B # $L = $A (arithmetically) shifted to the right by $B bits
Here are the arithmetic and logic instructions that operate on registers and take immediate data:
mov $L, I # $L = I (copy the immediate data I to $L)
add $L, $A, I # $L = $A + I
sub $L, $A, I # $L = $A - I
and $L, $A, I # $L = bitwise AND of $A and I
ior $L, $A, I # $L = bitwise (inclusive) OR of $A and I
eor $L, $A, I # $L = bitwise exclusive OR of $A and I
lsl $L, $A, I # $L = $A shifted to the left by I bits
lsr $L, $A, I # $L = $A shifted to the right by I bits
asr $L, $A, I # $L = $A (arithmetically) shifted to the right by I bits
Here are the instructions for accessing (loading data from and storing data to) memory:
loa $L, $A # $L = [contents of memory word at address $A]
sto $L, $A # [contents of memory word at address $L] = $A
Here are the comparison instructions whose result controls what happens when a branch instruction is executed:
cmp $A, $B # compare $A (left) and $B (right)
cmp $A, I # compare $A (left) and I (right)
Here are the jump and branch instructions that take a register operand (the address where we jump or branch, if the branch condition is met):
jmp $A # jump to address $A
beq $A # ... if left == right (in the most recent comparison)
bne $A # ... if left != right
bgt $A # ... if left > right (signed)
blt $A # ... if left < right (signed)
bge $A # ... if left >= right (signed)
ble $A # ... if left <= right (signed)
bab $A # ... if left > right (unsigned)
bbw $A # ... if left < right (unsigned)
bae $A # ... if left >= right (unsigned)
bbe $A # ... if left <= right (unsigned)
Here are the jump and branch instructions that take an immediate operand (the address where we jump or branch, if the branch condition is met):
jmp I # jump to address I
beq I # ... if left == right (in the most recent comparison)
bne I # ... if left != right
bgt I # ... if left > right (signed)
blt I # ... if left < right (signed)
bge I # ... if left >= right (signed)
ble I # ... if left <= right (signed)
bab I # ... if left > right (unsigned)
bbw I # ... if left < right (unsigned)
bae I # ... if left >= right (unsigned)
bbe I # ... if left <= right (unsigned)
The trap instruction halts the execution temporarily so that you may observe the register contents and memory for debugging purposes when your program is running:
trp # trap (break out of execution for debugging)
Finally, the halt instruction stops the processor:
hlt # halt execution
All right. That was the entire armlet instruction set.
Let us now outline some further conventions and hints.
When programming in assembly language, one of the recurrent curses is that
you run out of registers to hold the intermediate values in your computation.
In this case it is good to remember that the armlet has 65536 words of
memory available. Just be careful not to overwrite either the code of your
program or its input data!
Perhaps for the exercises we can agree on a convention that words at addresses from 60000 to 65535 are free for your code to use as scratch memory as you like. In fact, a recommended approach is to set up a stack where you can push values and pop them back in the reverse order they were pushed. Here is some sample code towards this end:
# Example armlet assembly code that uses a stack to save and recover contents
# of registers
#
# In the start of our code we reserve one of the registers, say $7,
# to act as a __stack pointer__ that contains the address of the
# first free slot in the stack.
#
# Let us start the stack at address 65535, and grow the stack towards
# lower addresses.
#
mov $7, 65535 # set up a stack
#
# ... Now suppose we are deep in user code, and suddenly need three
# registers, but can spare none ... How to get free registers?
#
# We can push the contents of any three registers to the stack.
# Say, let us push $0, $1, and $2.
#
sto $7, $0 # push $0 into the stack
sub $7, $7, 1
sto $7, $1 # push $1 into the stack
sub $7, $7, 1
sto $7, $2 # push $2 into the stack
sub $7, $7, 1
#
# Observe that after each store ("sto") to the stack, we update the
# stack pointer $7 so that it always points to a free slot in the stack.
# The combination of these operations (sto & sub) is called a "push" to
# the stack.
#
# ... Now we can use $0, $1, $2 as we like since their values are
# safely stored in the stack ...
#
# Suppose now we need the values back. In this case we simply pop
# the values out, one by one, in reverse order.
#
add $7, $7, 1
loa $2, $7 # pop $2 from the stack
add $7, $7, 1
loa $1, $7 # pop $1 from the stack
add $7, $7, 1
loa $0, $7 # pop $0 from the stack
#
# Observe that to correctly unwind the sequence of pushes, we need to
# update the stack pointer first and only then load ("loa") from the stack.
# The combination of these operations (add & loa) is called a "pop" from
# the stack.
#
# ... We can now resume computation with the original values of $0, $1, $2
# as if nothing happened ...
#