Round 8: Recursion
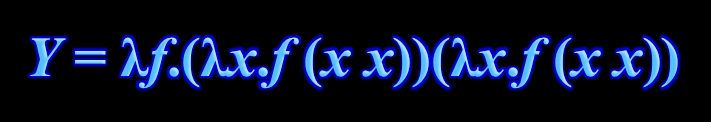
(Curry’s Y combinator.)
Learning objectives
In this round you will learn …
… that recursion is one of the basic programming principles to organize computations and data
… that the power of recursion stems from controlled self-reference that terminates at base cases
- in essence, we can implement a large computation (or data structure)
using smaller, self-similar, parts until the computation is so small so as to become trivial
… that many familiar mathematical objects and functions benefit from a recursive definition
- for example, a string of length \(n\)
either (i) is empty (when \(n=0\), the base case), or (ii) consists of a first character followed by a string of length \(n-1\) (when \(n\geq 1\), the recursive case)
recursive definitions lead to simple recursive functions that manipulate data or carry out a computation
recursive definitions admit mathematical analysis via mathematical induction (*)
… that recursion is naturally associated with a recursion tree that records all the stages of recursion
… that recursion is a natural tool to carry out exhaustive search
… how to use tail recursion to obtain efficiency
(Material that is marked with one or more asterisks (*) is good-to-know, but not critical to solving the exercises or passing the course.)