Refresher: Objects, references, and recursion recalled

Objects and references recalled

After a little bit of play, let us get back to work and review what actually happens when our circuit-building code runs, line by line. Here are the lines:

val a = new InputElement()
val b = new InputElement()
val g1 = new AndGate(a,b)
val g2 = new NotGate(a)
val g3 = new NotGate(b)
val g4 = new AndGate(g2,g3)
val out = new OrGate(g1,g4)

The first line is nothing much. We create an InputElement-object and have a reference to it stored in a.

val a = new InputElement()

As diagram we can display this as follows, where the blue arrow indicates that a refers to the newly created object.

The second line is pretty much the same story. Here it is important to remember that the two created InputGate-objects are independent of each other.

val a = new InputElement()
val b = new InputElement()

Let us record this in our diagram as well:

More interesting things start to happen when we executed the third line. Namely, we create a new AndGate-object whose inputs are to be the Gate-objects (or more precisely, the InputElement-objects!) referenced by a and b.

val a = new InputElement()
val b = new InputElement()
val g1 = new AndGate(a,b)

In our diagram we indicate this by recording that the in1- and in2-fields in the newly created AndGate-object now refer to the Gate-objects created.

The next line of code creates a new NotGate-object whose input is the Gate-object referenced by a.

val a = new InputElement()
val b = new InputElement()
val g1 = new AndGate(a,b)
val g2 = new NotGate(a)

Again we update the diagram to reflect what is going on:

The next line creates one more NotGate, which receives input from the Gate-object referenced by b:

val a = new InputElement()
val b = new InputElement()
val g1 = new AndGate(a,b)
val g2 = new NotGate(a)
val g3 = new NotGate(b)

Let us record this into our diagram:

Next, we create an AndGate-object whose inputs are the two NotGate-objects referenced by g2 and g3:

val a = new InputElement()
val b = new InputElement()
val g1 = new AndGate(a,b)
val g2 = new NotGate(a)
val g3 = new NotGate(b)
val g4 = new AndGate(g2,g3)

The resulting diagram is:

Finally, the last line creates an OrGate-object that receives input from the two AndGate-objects referenced by g1 and g4:

val a = new InputElement()
val b = new InputElement()
val g1 = new AndGate(a,b)
val g2 = new NotGate(a)
val g3 = new NotGate(b)
val g4 = new AndGate(g2,g3)
val out = new OrGate(g1,g4)

Let us record the last object into our diagram.

All right. That was seven lines of code, and seven diagrams.

Let us focus on the final diagram. Take a careful look at the references and recall what the circuit looks like:

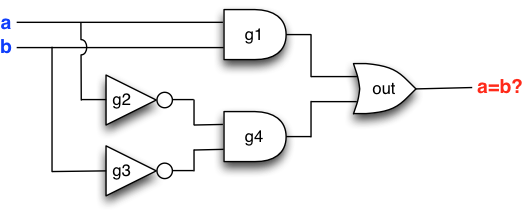
We observe that the structure of the circuit (the “wires” between gates) is encoded in the references between the created Gate-objects! This enables us to build circuits – as complex circuits as we like – by creating objects and passing references to existing objects to indicate the relationship of the new object to the existing objects. (For now our focus is on circuits, but later we will use the same trick to build far more intricate structures with data objects, that is to say, data structures.)

The diagram trick. To figure out what a piece of code does, it is without exception a rewarding workout to draw a diagram for yourself and update it step by step to witness what actually happens. Needless to say, diagrams are also useful from the perspective of designing your own code and data structures. When in doubt, draw diagrams to understand and keep track of what is going on. And do not worry if this takes time initially – with experience less and less diagrams will be necessary to figure out what is going on. Indeed, experienced programmers writes their own code to draw the diagrams automatically, if necessary.

Recursion recalled

Let us next study what happens when we set values to the input elements and then query the gates for values. Say, suppose we run the following lines of code:

a.set(false)
b.set(true)
out.value

Recall that the relevant objects look like this:

The first line of code sets the value of the InputElement-object referenced by a to false, and the second line sets the value of the InputElement-object referenced by b to true

The third line of code results in a sequence of recursive method invocations to compute the value of the Gate-object out. The diagram below summaries the computation. Each solid arrow is a method call that is made during the computation, and associated with these are dotted arrows in the reverse direction showing return values. By following the arrows from out.value to the input elements and back again you can trace the propagation from call to the callee.

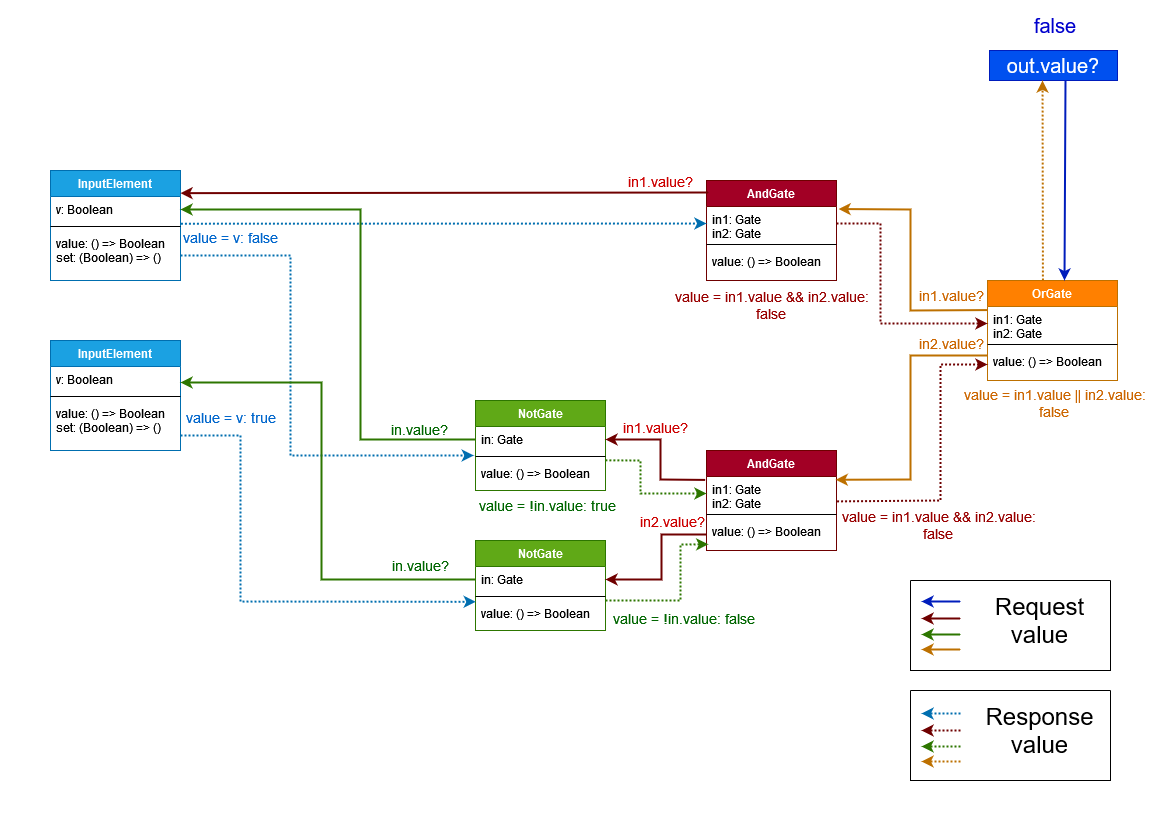
Observe how a method call leads to new method calls to determine the value of a gate. For example, to determine the value of out, we determine the value of both out.in1 and out.in2. The calls in turn lead to new calls that propagate across the structure towards the input elements. The propagation terminates at the input elements, which simply return their set values to the callees.

There is one special case that warrants attention at this point. Observe that the topmost AndGate-object makes only one recursive call. This is because the left operand of the &&-operator evaluates to false, and hence the evaluation can be short-circuited. (Indeed, regardless of the value of the right operand, the &&-expression will evaluate to false.) A similar situation occurs if the first operand of the operator || evaluates to true, in which case the value of the operator is true regardless of the value of the right operand, implying that evaluation can proceed without evaluating the right operand.

Let us focus on the dotted arrows that propagate the return values. Save for the short-circuited evaluations, the arrows propagate values through the circuit exactly as if we were operating a real physical circuit. Indeed, compare the dotted response arrows with the propagation in our previous figure:

Thus, we observe that the few lines of Scala code that it took to implement class Gate and its subclasses suffice not only to construct but also to operate the constructed circuits.