Numerical data

(An approximation of \(\pi\). )

To understand and work with numerical data, it is imperative to have a firm foundation on which to build. In our case such a foundation is our familiar positional number system.

The positional number system

In the positional number system (in the decimal base \(10\)), each nonnegative integer is represented as a sequence of decimal digits

\[0,\quad 1,\quad \ldots,\quad 9.\]

Consider, for example, the integer \(754\) that we represent in decimal by writing “\(754\)”.

Remark. The previous sentence does sound somewhat ridiculous at first reading. After all, \(754\) is \(754\), is it not? So let us think about this. Suppose we go back in history about two thousand years, and pay a visit to ancient Rome. The Romans knew \(754\) as “\(\mathrm{DCCLIV}\)”. The Romans had no idea about “\(754\)”. So perhaps there is something useful to “\(754\)” that we did not quite grasp yet.

In fact, both “\(754\)” and “\(\mathrm{DCCLIV}\)” are just references to a mathematical entity (the integer \(754\)). We could refer to this entity just as well with, say, “\({\color{blue}\blacksquare}{\color{red}\blacksquare}{\color{blue}\blacksquare}{\color{blue}\blacksquare}{\color{blue}\blacksquare}{\color{blue}\blacksquare}{\color{red}\blacksquare}{\color{red}\blacksquare}{\color{blue}\blacksquare}{\color{red}\blacksquare}\)”. Furthermore, we claim this representation would seem perfectly natural to us if we were from planet Zorp and instead of ten fingers had two antennae, one of them injecting \(\color{red}r\color{red}e\color{red}d\) ink and the other \(\color{blue}b\color{blue}l\color{blue}u\color{blue}e\) ink.

Much as we view “\(\mathrm{DCCLIV}\)” as cumbersome and awkward (try multiplying Roman numerals! – say, what is \(\mathrm{DCCLIV}\) times \(\mathrm{CDXXIX}\) ?), from the perspective of bits and data, the representation of \(754\) as “\(754\)” is not natural. Indeed, while we humans have ten fingers, and hence ten digits can be considered a natural choice, digital computers operate with bits, and hence two digits (”\(0\)” and “\(1\)”) are the natural choice. (The Zorpians naturally prefer “\({\color{red}\blacksquare}\)” and “\({\color{blue}\blacksquare}\)” in place of “\(0\)” and “\(1\)”.)

So what is a natural representation of \(754\), using bits?

Say, should we perhaps use the binary sequence “\(10110101101\)” or “\(1011110010\)” to represent \(754\), or perhaps something else?

The Zorpian natural choice to represent \(754\) appears to correspond to what we would write as “\(1011110010\)”, so perhaps the Zorpians know something that we may yet not know?

Also the console and the function tellAboutInt give us evidence that “\(1011110010\)” is the binary way to represent \(754\):

scala> tellAboutInt(754)
I am a 32-bit word that Scala views as having format 'Int' ...
... my bits are, in binary, (00000000000000000000001011110010)_2
... or equivalently, in hexadecimal, 0x000002F2
... Scala prints me out as 754
... I represent the signed decimal integer 754
... I represent the unsigned decimal integer 754

All right. So what is going on?

Let us first think about this in the familiar decimal system. We observe that we can decompose \(754\) into a sum of powers of the base \(B=10\) multiplied by the digits \(0\), \(1\), \(\ldots\), \(9\) as follows:

\begin{eqnarray} 754 & = &7\times 100 &+& 5\times 10 &+& &4\times 1 \\ & = &7\times 10^2 &+& 5\times 10^1 &+& &4\times 10^0. \end{eqnarray}

It is in fact precisely this decomposition that makes the positional number system extremely useful for computing. Namely, because of this decomposition, the positional number system is naturally suited for basic arithmetic such as integer addition, subtraction, multiplication, and division into a quotient and a remainder. (Recall the algorithms for arithmetic from your pre-university education.) Furthermore, the decomposition above is in fact unique. That is to say, there is no other way to express \(754\) as a sum of nonnegative integer powers of \(10\) multiplied by the digits \(0\), \(1\), \(\ldots\), \(9\).

The choice \(B = 10\) is merely a design choice to base the number system on a human convenience, the human hands.

Indeed, from a design perspective we can base the number system on any other integer \(B \geq 2\) of our choosing. Let us look at some examples first.

Example 1

In base \(B = 10\), the integer \(754\) is represented as

\begin{eqnarray} 754 &=& {\color{darkmagenta}7}\times 100 &+& {\color{darkmagenta}5}\times 10 &+& {\color{darkmagenta}4}\times 1 \\ &=& {\color{darkmagenta}7}\times 10^2 &+& {\color{darkmagenta}5}\times 10^1 &+& {\color{darkmagenta}4}\times 10^0. \end{eqnarray}

Example 2

In base \(B = 8\), the integer \(754\) is represented as

\begin{eqnarray} 754 &=& {\color{darkmagenta}1}\times 512 &+& {\color{darkmagenta}3}\times 64 &+& {\color{darkmagenta}6}\times 8 &+& {\color{darkmagenta}2}\times 1\\ &=& {\color{darkmagenta}1}\times 8^3 &+& {\color{darkmagenta}3}\times 8^2 &+& {\color{darkmagenta}6}\times 8^1 &+& {\color{darkmagenta}2}\times 8^0. \end{eqnarray}

Example 3

In base \(B=2\), the integer \(754\) is represented as

\begin{eqnarray} \!754\!&=&\! {\color{darkmagenta}1}\times 512 \!&{\small +}&\! {\color{darkmagenta}0}\times 256 \!&{\small +}&\! {\color{darkmagenta}1}\times 128 \!&{\small +}&\! {\color{darkmagenta}1}\times 64 \!&{\small +}&\! {\color{darkmagenta}1}\times 32 \!&{\small +}&\! {\color{darkmagenta}1}\times 16 \!&{\small +}&\! {\color{darkmagenta}0}\times 8 \!&{\small +}&\! {\color{darkmagenta}0}\times 4 \!&{\small +}&\! {\color{darkmagenta}1}\times 2 \!&{\small +}&\! {\color{darkmagenta}0}\times 1\\ \!&=&\! {\color{darkmagenta}1}\times 2^9 \!&{\small +}&\! {\color{darkmagenta}0}\times 2^8 \!&{\small +}&\! {\color{darkmagenta}1}\times 2^7 \!&{\small +}&\! {\color{darkmagenta}1}\times 2^6 \!&{\small +}&\! {\color{darkmagenta}1}\times 2^5 \!&{\small +}&\! {\color{darkmagenta}1}\times 2^4 \!&{\small +}&\! {\color{darkmagenta}0}\times 2^3 \!&{\small +}&\! {\color{darkmagenta}0}\times 2^2 \!&{\small +}&\! {\color{darkmagenta}1}\times 2^1 \!&{\small +}&\! {\color{darkmagenta}0}\times 2^0. \end{eqnarray}

We observe a pattern, namely successive integer powers of the base \(B\) multiplied with \({\color{darkmagenta}d}{\color{darkmagenta}i}{\color{darkmagenta}g}{\color{darkmagenta}i}{\color{darkmagenta}t}{\color{darkmagenta}s}\) ranging in \(\{0,1,\ldots,B-1\}\).

Let us state a general form of this observation as a fact, which the mathematically inclined readers are invited to verify using induction on \(d\).

Note

Fact. Every integer \(a\) in the range \(0\leq a\leq B^d-1\) can be uniquely represented using \(d\) digits in base \(B\) as

\[a = {\color{darkmagenta}a_{\color{darkmagenta}d\color{darkmagenta}-\color{darkmagenta}1}}\times B^{d-1} + \ldots + {\color{darkmagenta}a_{\color{darkmagenta}2}}\times B^{2} + {\color{darkmagenta}a_{\color{darkmagenta}1}}\times B^{1} + {\color{darkmagenta}a_{\color{darkmagenta}0}}\times B^{0}\]

such that \({\color{darkmagenta}a_{\color{darkmagenta}j}}\in \{0,1,\ldots,B-1\}\) holds for all \(0\leq j\leq d-1\). We write this succinctly as

\[a = ({\color{darkmagenta}a_{\color{darkmagenta}d\color{darkmagenta}-\color{darkmagenta}1}}, {\color{darkmagenta}a_{\color{darkmagenta}d\color{darkmagenta}-\color{darkmagenta}2}}, \ldots, {\color{darkmagenta}a_{\color{darkmagenta}0}})_B.\]

The digit \({\color{darkmagenta}a_{\color{darkmagenta}d\color{darkmagenta}-\color{darkmagenta}1}}\) is called the most significant digit and the digit \({\color{darkmagenta}a_{\color{darkmagenta}0}}\) is called the least significant digit.

Example

Let us write the three examples above using the more succinct notation. We have:

\[754 = ({\color{darkmagenta}7}, {\color{darkmagenta}5}, {\color{darkmagenta}4})_{10} = ({\color{darkmagenta}1}, {\color{darkmagenta}3}, {\color{darkmagenta}6}, {\color{darkmagenta}2})_8 = ({\color{darkmagenta}1}, {\color{darkmagenta}0}, {\color{darkmagenta}1}, {\color{darkmagenta}1}, {\color{darkmagenta}1}, {\color{darkmagenta}1}, {\color{darkmagenta}0}, {\color{darkmagenta}0}, {\color{darkmagenta}1}, {\color{darkmagenta}0})_2\]

When there is no risk of confusion, in particular when the base \(B \leq 10\), we can lighten the notation by removing the commas:

\[754 = ({\color{darkmagenta}7}{\color{darkmagenta}5}{\color{darkmagenta}4})_{10} = ({\color{darkmagenta}1}{\color{darkmagenta}3}{\color{darkmagenta}6}{\color{darkmagenta}2})_8 = ({\color{darkmagenta}1}{\color{darkmagenta}0}{\color{darkmagenta}1}{\color{darkmagenta}1}{\color{darkmagenta}1}{\color{darkmagenta}1}{\color{darkmagenta}0}{\color{darkmagenta}0}{\color{darkmagenta}1}{\color{darkmagenta}0})_2\]

We have now in place some examples and the notation, but we have not yet reviewed how to actually determine the representation in base \(B\).

Let us think about this. Suppose we have to compute the representation in base \(2\). Say, we have \(999\) in decimal given to us, and we are asked to determine the representation of \(999\) in base \(2\). How do we proceed?

Let us review yet again what must be done. We only know \(999\), and somehow we must come up with the representation

\[999 = {\color{darkmagenta}1}\times 2^{9} + {\color{darkmagenta}1}\times 2^{8} + {\color{darkmagenta}1}\times 2^{7} + {\color{darkmagenta}1}\times 2^{6} + {\color{darkmagenta}1}\times 2^{5} + {\color{darkmagenta}0}\times 2^{4} + {\color{darkmagenta}0}\times 2^{3} + {\color{darkmagenta}1}\times 2^{2} + {\color{darkmagenta}1}\times 2^{1} + {\color{darkmagenta}1}\times 2^{0}.\]

How do we do this, knowing only \(999\)? Let us study the representation in detail. Could we perhaps somehow recover only one digit, say the least significant digit? (That is, the \({\color{darkmagenta}c\color{darkmagenta}o\color{darkmagenta}e\color{darkmagenta}f\color{darkmagenta}f\color{darkmagenta}i\color{darkmagenta}c\color{darkmagenta}i\color{darkmagenta}e\color{darkmagenta}n\color{darkmagenta}t}\) of \(2^{0} = 1\).) We observe that all the other powers of \(2\) in the decomposition are (clearly!) divisible by \(2\), except for \(2^{0} = 1\). Thus, we can \({\color{red}c\color{red}o\color{red}l\color{red}l\color{red}e\color{red}c\color{red}t}\) and observe that everything except possibly the last term is divisible by \(2\):

\[999 = {\color{red}(}{\color{darkmagenta}1}\times 2^{8} + {\color{darkmagenta}1}\times 2^{7} + {\color{darkmagenta}1}\times 2^{6} + {\color{darkmagenta}1}\times 2^{5} + {\color{darkmagenta}1}\times 2^{4} + {\color{darkmagenta}0}\times 2^{3} + {\color{darkmagenta}0}\times 2^{2} + {\color{darkmagenta}1}\times 2^{1} + {\color{darkmagenta}1}\times 2^{0}{\color{red})}\times 2 + {\color{darkmagenta}1}\times 1.\]

In particular, the remainder of the division of \(999\) by \(2\) equals the least significant digit in the representation of \(999\) in base \(2\).

So how do we get the other digits? Observe that what we have \({\color{red}c\color{red}o\color{red}l\color{red}l\color{red}e\color{red}c\color{red}t\color{red}e\color{red}d}\) is exactly the quotient of the division of \(999\) by \(2\).

What we have now is a procedure for determining the decomposition of \(999\) (or any other nonnegative integer) in base \(2\): We repeatedly divide by \(2\), record the \({\color{darkmagenta}r\color{darkmagenta}e\color{darkmagenta}m\color{darkmagenta}a\color{darkmagenta}i\color{darkmagenta}n\color{darkmagenta}d\color{darkmagenta}e\color{darkmagenta}r}\), and then (recursively) process the \({\color{red}q\color{red}u\color{red}o\color{red}t\color{red}i\color{red}e\color{red}n\color{red}t}\) until the quotient equals \(0\). This procedure recovers us the digits in order from least significant to most significant.

Let us try this out with \(999\). Here we go:

\[\begin{split}999&={\color{red}4\color{red}9\color{red}9}\times 2 + {\color{darkmagenta}1}\\ 499&={\color{red}2\color{red}4\color{red}9}\times 2 + {\color{darkmagenta}1}\\ 249&={\color{red}1\color{red}2\color{red}4}\times 2 + {\color{darkmagenta}1}\\ 124&={\color{red}6\color{red}2}\times 2 + {\color{darkmagenta}0}\\ 62&={\color{red}3\color{red}1}\times 2 + {\color{darkmagenta}0}\\ 31&={\color{red}1\color{red}5}\times 2 + {\color{darkmagenta}1}\\ 15&={\color{red}7}\times 2 + {\color{darkmagenta}1}\\ 7&={\color{red}3}\times 2 + {\color{darkmagenta}1}\\ 3&={\color{red}1}\times 2 + {\color{darkmagenta}1}\\ 1&={\color{red}0}\times 2 + {\color{darkmagenta}1}\end{split}\]

We observe that what we have recovered is exactly the digits of the decomposition \(999 = ({\color{darkmagenta}1\color{darkmagenta}1\color{darkmagenta}1\color{darkmagenta}1\color{darkmagenta}1\color{darkmagenta}0\color{darkmagenta}0\color{darkmagenta}1\color{darkmagenta}1\color{darkmagenta}1})_2\).

We record a general form of what is above as a fact:

Note

Fact. We can determine the representation \((a_{d-1}, a_{d-2}, \ldots, a_0)_{B}\) of an integer \(0\leq a\leq B^{d}-1\) from the quotient \(q=\lfloor a/B\rfloor\) and the remainder \(r = a\bmod b\) when we divide \(a\) by the base \(B\). Then the remainder \(r\) gives the least significant digit \(a_0\), and the more significant digits \(a_{d-1}, \ldots, a_2, a_1\) are obtained by recursively processing the quotient \(q\) as long as \(q\) remains positive.

To see this, let us group the terms in the definition:

\[\begin{split}a &= a_{d-1}\times B^{d-1} + \ldots + a_2\times B^2 + a_1\times B^1 + a_0\times B^0 \\ &= (a_{d-1}\times B^{d-2} + \ldots + a_2\times B + a_1)B + a_0\\ &= qB + r.\end{split}\]

In Scala programming terms, the previous fact leads immediately to a recursive function that computes the representation of a nonnegative \(a\) in base \(B\):

def toBaseB(a: Int, b: Int): Seq[Int] =
  require(a >= 0 && b >= 2)
  val r = a%b
  val q = a/b
  if q > 0 then toBaseB(q,b) :+ r  else Seq(r)
end toBaseB

Remark. Do not worry if you are not comfortable with recursive functions yet. We will get plenty of drill on recursion during later rounds.

Here is an implementation written in more procedural style:

def toBaseB(a: Int, b: Int): Seq[Int] =
  require(a >= 0 && b >= 2)
  var r = a%b
  var q = a/b
  var rr = Seq(r)
  while q > 0 do
    r = q%b
    q = q/b
    rr = r +: rr
  end while
  rr
end toBaseB

Determining representations in any base \(B\) you like is now easy:

scala> toBaseB(754,10)
res: Seq[Int] = List(7, 5, 4)

scala> toBaseB(754,2)
res: Seq[Int] = List(1, 0, 1, 1, 1, 1, 0, 0, 1, 0)

scala> toBaseB(754,8)
res: Seq[Int] = List(1, 3, 6, 2)

scala> toBaseB(754,16)
res: Seq[Int] = List(2, 15, 2)

Conversely, we can reconstruct an integer from its base \(B\) representation as a sequence \((a_{d-1}, a_{d-2}, \ldots, a_0)_B\) of digits by multiplying each digit \(a_j\) with the corresponding power \(B^j\) and taking the sum of the products. Here is an idiomatic implementation in Scala (with plenty of practice in idioms to follow later):

def fromBaseB(a: Seq[Int], b: Int): Int =
  require(b >= 2 && a.forall(_ >= 0) && a.forall(_ <= b-1))
  (a.foldRight (0,1) { case (aj,(r,bj)) => (r+aj*bj,bj*b) })._1
end fromBaseB

Here is an implementation written in more procedural style:

def fromBaseB(a: Seq[Int], b: Int): Int =
  require(b >= 2 && a.forall(_ >= 0) && a.forall(_ <= b-1))
  val d = a.length
  var j = 0
  var bj = 1
  var z = 0
  while j < d do
    z = z+a(d-1-j)*bj
    j = j+1
    bj = bj*b
  end while
  z
end fromBaseB

Working out what a base \(B\) representation means in decimal is now easy:

scala> fromBaseB(Seq(1, 0, 1, 1, 1, 1, 0, 0, 1, 0), 2)
res: Int = 754

scala> fromBaseB(Seq(1, 3, 6, 2), 8)
res: Int = 754

scala> fromBaseB(Seq(2, 15, 2), 16)
res: Int = 754

scala> fromBaseB(Seq(7, 5, 4), 10)
res: Int = 754

Caveat. Because of internal limitations of the type Int, the function fromBaseB fails unless \(0\leq a\leq 2^{31}-1\).

Beyond base 10

If the base \(B\) is larger than \(10\), for example, \(B = 16\), the convention is to use the Roman alphabet to extend the digits beyond the Arabic numerals \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\). For example, with \(B = 16\) the convention is to use \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\), \(\mathrm{A}\), \(\mathrm{B}\), \(\mathrm{C}\), \(\mathrm{D}\), \(\mathrm{E}\), \(\mathrm{F}\) as the \(16\) digits. That is to say, in base \(B = 16\) we have

\begin{eqnarray} 754 &=& 2\times 256 &+& 15\times 16 &+& 2\times 1 \\ &=& 2\times 16^{2} &+& \mathrm{F}\times 16^{1} &+& 2\times 16^{0} \end{eqnarray}

or more succinctly

\[\begin{split}754 &= (2,15,2)_{16} \\ &= (2,\mathrm{F},2)_{16} \\ &= (2\mathrm{F}2)_{16}.\end{split}\]

Binary, octal, decimal, hexadecimal

Note

The representation of an integer \(a\) in base \(B = 10\) is called the decimal representation of \(a\). Similarly, base \(B = 16\) is the hexadecimal representation, base \(B = 8\) the octal representation, and base \(B = 2\) the binary representation of \(a\). The digits in the binary representation are called binary digits or bits.

Serendipity of hexadecimal

So exactly why did we bother with hexadecimal?

In short, hexadecimal is a programmer’s convenient shorthand to numbers in binary. Say, it is far more concise and readable to write \((\mathrm{FAE}362\mathrm{A}9)_{16}\) than \((11111010111000110110001010101001)_2\) when we need to express a 32-bit number in binary.

The mathematically serendipitous fact of the matter is that \(16 = 2^{4}\), implying that in the hexadecimal (base \(16\)) representation of an integer \(x\), each hexadecimal digit corresponds to a group of \(4\) binary digits in the binary (base \(2\)) representation of \(x\).

The exact correspondence is as follows:

In particular, it is easy to convert between binary and hexadecimal – just follow the table, which many a more seasoned programmer knows by heart.

Converting between binary and hexadecimal is now an effortless routine, just proceed one group of four bits (one hexadecimal digit) at a time:

Remark. Of course there is nothing special about \(16\) from a mathematical perspective apart from the fact that it is a power of \(2\). Octal (base \(8\)) is also a power of \(2\), and can be used to represent groups of \(3\) bits since \(2^3 = 8\).

Bit positions in a word

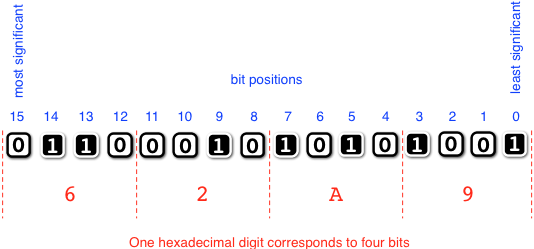
Now that we know hexadecimal, let us start studying the bits in a word. For this we need to agree on a convention on how to index the bit positions in a word.

Indexing convention for bit positions in a word. In accordance with the binary number system and established convention, the bit positions in a \(b\)-bit word are indexed starting from the least significant bit (which has index \(0\)) to the most significant bit (which has index \(b - 1\)).

Hexadecimal in Scala

Scala programs and the console default to numerical values in decimal representation:

scala> val x = 999
x: Int = 999

Internally, Scala of course operates in binary. The decimal input/output is just a convenience that hides the bits from programmers who do not know better. Accordingly, for more informed programmers, Scala is perfectly happy to accept numerical input in hexadecimal if we signal this by prefixing the input with “0x”:

scala> val y = 0x3E7
y: Int = 999

Note that Scala still reports back to us in decimal. In particular, Scala reports back 999 because

\[999 = (999)_{10} = (1111100111)_{2} = (3\mathrm{E}7)_{16}.\]

We can now carry out all our computations in hexadecimal if we feel like it:

scala> 0x3E7 + 0x1
res: Int = 1000

scala> 0x3E7 * 0xA
res: Int = 9990

The annoying thing is of course that the result is displayed in decimal. When working with bits, we usually want to see the binary representation (in hexadecimal) of whatever we are working with.

To display an Int in hexadecimal in Scala, we can use the string formatting tools available in Scala StringOps:

def toHexString(v: Int): String = "0x%X".format(v)

The function above uses the method format in class String to format v as a string of hexadecimal digits prefixed by "0x". The hexadecimal formatting of the bits in v is in particular requested by the format specifier "%X".

scala> toHexString(754)
res: String = 0x2F2

scala> toHexString(999)
res: String = 0x3E7

scala> toHexString(0x3E7)
res: String = 0x3E7

(We will discuss method format and formatted string output in more detail later.)

Forcing and toggling bits in a word

Now that we have basic reading and writing skills in binary (that is, we know how to use the hexadecimal shorthand), the next skill is to be able to operate on the bits in a word. That is to say, we want to take a word and produce from it a word where some of the bits have been changed as we instruct.

Boolean operations on bits. We can operate on individual bits using the Boolean operations AND (”&”), OR (”|”), XOR (”^”), and NOT (”~”) defined as follows:

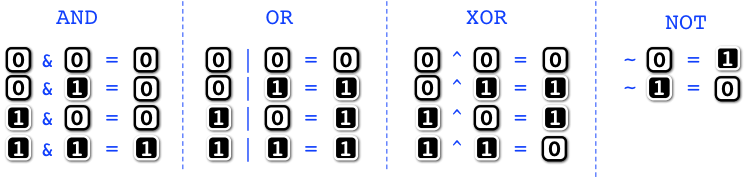
Or what is the same,

• AND is the minimum of its two operands,

• OR is the maximum of its two operands,

• XOR is the parity of the sum of its two operands (either even or odd), and

• NOT complements its operand from 0 to 1, and from 1 to 0.

Forcing and toggling the value of a bit. Let us write \(x\) for an unknown Boolean value (either 0 or 1), and let \(\bar x\) be the complement of \(x\) (either 1 or 0). By inspection we observe that the following equations hold for the Boolean operators AND, OR, and XOR:

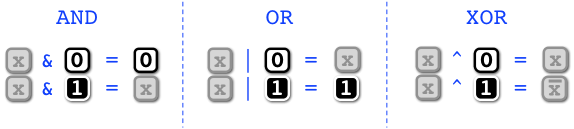
Let us now justify these equations and put them to use in forcing and toggling unknown bits.

Since AND is equivalent to minimum, if the known operand is 0, then the result will be 0 regardless of the value of the unknown operand. On the other hand, if the known operand is 1, then the result will be equal to the unknown value. Thus, we can use AND to force bits to 0. Forcing a bit to 0 is alternatively called resetting, masking, or clearing the bit.

Since OR is equivalent to maximum, if the known operand is 1, then the result will be 1 regardless of the value of the unknown operand. On the other hand, if the other operand is 0, then the result will be equal to the unknown value. Thus, we can use OR to force bits to 1. Forcing a bit to 1 is alternatively called setting the bit.

The equations for XOR can be verified by inspection of all cases. If the known operand is 0, then the result will have identical value with the unknown operand. If the known operand is 1, then the value of the result will be the complement of the unknown operand. Thus, we can use XOR to toggle the value of bits. Toggling the value of a bit is alternatively called complementing the bit.

Boolean operations on words. When the left and right operands are words, the Boolean operators by convention operate independently on each bit position. That is, the bit at position j of the result word is the AND/OR/XOR of the bits at position j of the operand words. Here is an illustration:

The bitwise NOT accepts only one word as operand, and the bit at position \(j\) of the result word is the NOT of the bit at position \(j\) of the operand word. Here is an illustration:

Forcing and toggling the bits in a word. Using bitwise operations, we can now operate on a word to produce another word whose bits have been changed (forced or toggled) in relation to the original word as we instruct. In fact, an arbitrary bitwise operation requires at most one bitwise AND (to force bits to value 0), at most one bitwise OR (to force bits to value 1), and at most one bitwise XOR (to toggle bits).

Here is an illustration of forcing and toggling the bits of an 8-bit word:

In Scala we of course have to specify what we want in hexadecimal. The following example operates on some of the 32 bits of an Int and returns the result:

def bitExample(x: Int): Int =
  // Forcing bits to 0 with AND:

  val x_with_forced_0s = x & 0x7AFE3FFF

  //
  // 0x7AFE3FFF is 01111010111111100011111111111111 in binary
  //
  //               10987654321098765432109876543210 (bit positions)
  //                3         2         1
  //
  // Thus, what is above forces the bits at positions
  // 31, 26, 24, 16, 15, and 14 to 0.
  //


  // Forcing bits to 1 with OR:

  val x_with_forced_0s_and_1s = x_with_forced_0s | 0x02380A70

  //
  // 0x02380A70 is 00000010001110000000101001110000 in binary
  //
  //               10987654321098765432109876543210 (bit positions)
  //                3         2         1
  //
  // Thus, what is above forces the bits at positions
  // 25, 21, 20, 19, 11, 9, 6, 5, and 4 to 1.
  //


  // Toggling bits with XOR:

  val x_with_forces_and_toggles = x_with_forced_0s_and_1s ^ 0x18C2008A

  //
  // 0x18C2008A is 00011000110000100000000010001010 in binary
  //
  //               10987654321098765432109876543210 (bit positions)
  //                3         2         1
  //
  // Thus, what is above toggles the bits at positions
  // 28, 27, 23, 22, 17, 7, 3, and 1.
  //

  x_with_forces_and_toggles
    // return the result with desired forces and toggles
end bitExample

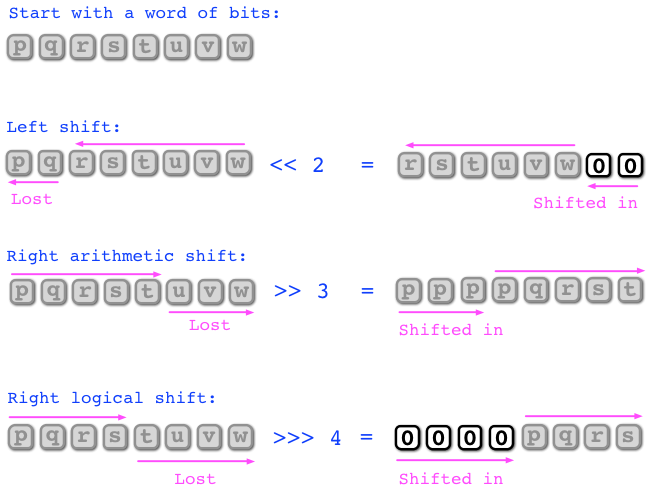
Shifting the bits in a word

The bitwise operations AND, OR, XOR, NOT operate independently on each bit position. These operations are frequently combined with shift operations that move the bits in a word either left or right a given number of positions. In more precise terms, the shift operations are as follows:

Left shift. The left shift of a word shifts all the bits to the left by a given number of positions, shifting in from the right equally many 0-bits, and losing the bits that get shifted out of the word in the left. In Scala, the operator “<<” gives the left shift of a word (the left operand) by a nonnegative amount (the right operand).

Right arithmetic shift. The right arithmetic shift of a word shifts all the bits to the right by a given number of positions, shifting from the right in equally many bits whose value agrees with the most significant bit, and losing the bits that get shifted out of the word in the right. In Scala, the operator “>>” gives the right arithmetic shift of a word (the left operand) by a nonnegative amount (the right operand).

Right logical shift. The right logical shift is exactly as the right arithmetic shift, except that the bits shifted in from the right are always 0-bits. In Scala, the operator “>>>” gives the right logical shift of a word (the left operand) by a nonnegative amount (the right operand).

Here is an illustration of the shift operations on an 8-bit word:

Four basic tricks of the trade

Trick: Getting the value of the bit at position \(j\). Suppose we have a word x and we want to read the value of the bit at position j, where j is a nonnegative integer. Then, the idiom (x >> j)&1 evaluates to either 0 or 1, in agreement with the value of the bit at position j. (Note that the Scala type of the value depends on the types of x and j.)

scala> val x = 0x3A  // 111010 in binary
x: Int = 58

scala> (x >> 0)&1    // value of bit at position 0
res: Int = 0

scala> (x >> 1)&1    // value of bit at position 1
res: Int = 1

scala> (x >> 2)&1    // value of bit at position 2
res: Int = 0

scala> (x >> 3)&1    // ...
res: Int = 1

scala> (x >> 4)&1
res: Int = 1

scala> (x >> 5)&1
res: Int = 1

scala> (x >> 6)&1
res: Int = 0

Trick: Getting a word where exactly the bit at position \(j\) is set to value 1. Another recurrent idiom is “1 << j” where j is a nonnegative integer. The result of 1 << j is an Int where exactly the bit at position \(j\) has value 1, and all other bit positions have value 0.

Trick: Left shift as multiplication. The left shift by \(j \geq 0\) positions corresponds to multiplying the word by \(2^j\). Indeed, think about the representation in the binary number system – the bit at position \(i\) is the coefficient of \(2^i\), so left-shifting by \(j\) moves this bit to position \(i + j\), where it is the coefficient of \(2^{i + j}\).

scala> val x = 52
x: Int = 52

scala> x << 3       // x * 8
res: Int = 416

Trick: Right arithmetic shift as division. The right arithmetic shift by \(j \geq 0\) positions corresponds to dividing the word by \(2^j\) and rounding down.

scala> val x = -123
x: Int = -123

scala> x >> 3    // x/8 rounded down
res: Int = -16

scala> val x = 123
x: Int = 123

scala> x >> 3    // x/8 rounded down
res: Int = 15

Note

When working with Byte and Short, note that these types (8 and 16 bits respectively) will be promoted to Int (32 bits) before bit-wise operators re applied. Because the conversion preserves the sign of the number stored, this has the result that for example the right logical shift (>>>) may not always work as expected, as it is applied to 32 bits instead of 8 or 16. To be sure to get the expected result when right-shifting a Byte or Short the results must be properly masked before the operation. This masking is done by a logical and with as many ones as the bits in a byte or short. For a byte we need eight bits, so the mask is 0xFF and for a short 16 bits, meaning the mask is 0xFFFF. For example, if you want to shift the Byte stored in x two steps right, you must first mask x accordingly: (x & 0xFF)>>>2.

Packing and unpacking bits

Many binary formats require us to pack the bits of multiple data items into a word, and conversely unpack the word into multiple data items. Typically each data item is a word in itself.

Example 1. Packings where each data item is a 1-bit word occur frequently in programming that they have a dedicated name. Such a packing is called a bit map. (Although the term is used also to refer to somewhat more general packings.) We will study bit maps in more detail in the exercises.

Example 2. Suppose we want to pack three data items into a 64-bit word. Each data item is a word that is to be packed as follows:

• A 1-bit word, called the sign, to be packed into the most significant bit (position 63).

• An 11-bit word, called the biased exponent, to be packed into the next most significant bits (positions 62 to 52).

• A 52-bit word, called the trailing significand, to be packed into the next most significant bits (positions 51 to 0).

Below is an implementation of the packing and unpacking routines in Scala. Type Long in Scala is a 64-bit word, and accordingly is the type for the packed word. We use the least significant bits of each of the words sign, bexp, and tsig to store the data items in unpacked form. Before packing we also check that the data items are good in the sense that all bits beyond the relevant least significant bits are 0-bits in each data item.

def bitPackExample(sign: Int, bexp: Int, tsig: Long) =
  require((sign & ~0x1) == 0 &&
          (bexp & ~0x7FF) == 0 &&
          (tsig & ~0x000FFFFFFFFFFFFFL) == 0L) // check the data items
  val packed = (sign.toLong << 63)|
               (bexp.toLong << 52)|
               tsig                     // pack the data items into a long
  packed
end bitPackExample

def bitUnpackExample(packed: Long) =
  val sign = ((packed >> 63) & 0x1L).toInt    // unpack sign
  val bexp = ((packed >> 52) & 0x7FFL).toInt  // unpack biased exponent
  val tsig = packed & 0x000FFFFFFFFFFFFFL     // unpack trailing significand
  (sign, bexp, tsig)
end bitUnpackExample

Here is an example how packing and unpacking works:

scala> val p = bitPackExample(1,52,1987654235678L)
p: Long = -8989182868577274338

scala> bitUnpackExample(p)
res: (Int, Int, Long) = (1,52,1987654235678)

Numerical computation (*)

Let us now step away from the binary world for a moment. In particular, let us reflect about our everyday needs as practicioners in the natural sciences and engineering. Numerical computation requires us to manipulate numbers with varying magnitudes and varying degrees of precision, be it data from physical experiments, or synthetic data used to run a simulation, such as the rendering of computer graphics. For example, we may require an approximation of \(\pi\) in our computations:

\[3.141592653589793\]

More generally, numbers in scientific computation routinely range across many orders of magnitude from very small numbers, such as Planck’s constant (\(h = 6.62606957\times 10^{-34}\mathrm{Js}\)), to very large numbers, such as Avogadro’s number (\(N = 6.02214129\times 10^{23}\mathrm{mol}^{-1}\)).

To illustrate the difference in scale, let us display these constants as plain decimal numbers without the exponential notation:

//  602214129000000000000000.0 /mol
//                         3.141592653589793
//                         0.00000000000000000000000000000000062606957 Js

In fact, large differences in magnitude can also occur in an everyday computing context. For example, a bulk DDR3-1066 SDRAM memory module can transfer data at a peak rate of 1.066 billion 64-bit word transfers per second. Thus, at peak rate, one 64-bit word is transferred every 0.938 nanoseconds. (Amusingly, you may want to recall that in one nanosecond light travels about 30 centimeters.) To contrast this speed, let us calculate the total number of words which can be held by modern memory hardware. For instance the Oracle Sparc M6-32 server can accommodate up to 32 tebibytes of main memory. Measured in 64-bit words, 32 tebibytes is exactly 4398046511104 words of main memory.

Here is an illustration of the difference in scale:

//  4398046511104.0 words
//              0.000000000938 s/word

If we multiply the main memory capacity with the peak transfer rate, we observe that it takes more than one hour for a single thread to scan through the main memory.

The take-home message from this motivation is that both routine scientific computation and everyday computing practice require us to span many orders of magnitude in terms of the numerical computations involved.

Let us now return to think about bits and data.

In fact, it appears we are facing quite a challenge.

Challenge. To enable fast numerical computation in hardware, we want to use a fixed-length format (such as a 64-bit word) to represent numbers with varying magnitudes and varying precision. This presents a challenge since, as we know, a 64-bit word can be in only \(2^{64} = 18446744073709551616\) distinct states. In particular, we can represent only at most 18446744073709551616 distinct numbers with 64 bits. In particular, 64 bits (or any fixed number of bits for that matter) does not suffice to represent a number with arbitrary magnitude or arbitrary precision.

Yet, in practice a great deal of numerical computation is successfully carried out using fixed-length binary formats. For example, essentially all of computer graphics is rendered using fixed-precision arithmetic.

To understand the tradeoffs involved, let us first return to study the positional number system again.

Radix point notation (*)

The positional number system enables us to represent not only integers, but also numbers with a fractional part. Indeed, we can represent a number such as

\[574.6312\]

by writing a sequence of decimal digits \(0, 1, \ldots, 9\) punctuated by at most one radix point “\(.\)” whose role is to provide a point of reference to the scale of the number. In more precise terms, the role of the radix point is to split the representation into its integer part (to the left of the radix point) and its fractional part (to the right of the radix point):

\[{\color{darkmagenta}5\color{darkmagenta}7\color{darkmagenta}4}.{\color{darkmagenta}6\color{darkmagenta}3\color{darkmagenta}1\color{darkmagenta}2} = {\color{darkmagenta}5}\times 10^{2} + {\color{darkmagenta}7}\times 10^{1} + {\color{darkmagenta}4}\times 10^{0} + {\color{darkmagenta}6}\times 10^{-1} + {\color{darkmagenta}3}\times 10^{-2} + {\color{darkmagenta}1}\times 10^{-3} + {\color{darkmagenta}2}\times 10^{-4}\]

That is, the digits to the left of the radix point receive as coefficients nonnegative integer powers of the base \(B = 10\), starting with \(10^0 = 1\), and the digits to the right of the radix point receive as coefficients negative integer powers of the base, starting with \(10^{-1} = 1/10\). If we omit the radix point then it is understood that the fractional part has only \(0\)-digits, that is, the number is an integer.

Normalized representation. In many cases it is useful to normalize the radix-point representation of a positive number by collecting the coefficient of its leading non-\(0\) digit. For example, the leading non-\(0\) digit of \(574.6312\) is \(5\), with coefficient \(10^2\). Thus, the normalized form of \(574.6312\) is

\[{\color{darkmagenta}5}.{\color{darkmagenta}7\color{darkmagenta}4\color{darkmagenta}6\color{darkmagenta}3\color{darkmagenta}1\color{darkmagenta}2}\times 10^{2} = ({\color{darkmagenta}5}\times 10^{0} + {\color{darkmagenta}7}\times 10^{-1} \!+ {\color{darkmagenta}4}\times 10^{-2} \!+ {\color{darkmagenta}6}\times 10^{-3} \!+ {\color{darkmagenta}3}\times 10^{-4} \!+ {\color{darkmagenta}1}\times 10^{-5} \!+ {\color{darkmagenta}2}\times 10^{-6}) \times 10^{2}\]

In fact, every positive real number has a normalized radix-point representation using an infinite sequence of digits after the radix point. This representation is unique if we agree to use a sequence that has a finite number of non-\(0\) digits, with the trailing infinite sequence of \(0\)-digits omitted, whenever such a sequence exists. For example, we agree that \(2/5\) is represented by the normalized sequence \(4\times 10^{-1}\) and not the normalized sequence \(3.9999\ldots\times 10^{-2}\). (Here the three dots “\(\ldots\)” indicate that the sequence of digits is infinite.)

Representing rational numbers in radix point. A further fact about the radix-point representation is that not all rational numbers can be accurately represented by a finite sequence of digits. For example,

\[1/3 = 3.33333\ldots\times 10^{-1}\]

requires an infinite sequence of digits for accurate representation. What is true however, is that the (normalized) radix-point representation of every positive rational number consists of a finite prefix of digits followed by an infinite periodic part with a finite period. (Here we allow the periodic part to consist of only \(0\)-digits.) For example,

\[96/7 = 1.3714285714285714285\ldots\times 10^{1}\]

where the prefix (without the radix point) is \(13\) and the sequence \(714285\) forms the infinitely repeating periodic part. Conversely, every real number with such a periodic radix-point representation is in fact a rational number. If you are familiar with modular arithmetic and want to practice your skills, you may want to think about why this is the case.

Arbitrary base. Above we again worked in the decimal base (base \(10\)) for reasons of familiarity, but the radix point representation generalizes to an arbitrary integer base \(B \geq 2\).

An arbitrary positive real number has a unique normalized radix-point representation in base \(B\) in the form

\[({\color{darkmagenta}d_{\color{darkmagenta}0}}.{\color{darkmagenta}d_{\color{darkmagenta}1}\color{darkmagenta}d_{\color{darkmagenta}2}\color{darkmagenta}d_{\color{darkmagenta}3}}\ldots )_{B} \times B^{e} = ( {\color{darkmagenta}d_{\color{darkmagenta}0}}\times B^{0} + {\color{darkmagenta}d_{\color{darkmagenta}1}}\times B^{-1} + {\color{darkmagenta}d_{\color{darkmagenta}2}}\times B^{-2} + {\color{darkmagenta}d_{\color{darkmagenta}3}}\times B^{-3} + \ldots )\times B^{e}\]

where the exponent \(e\) is an integer and the digits of the significand \({\color{darkmagenta}d_{\color{darkmagenta}0}}.{\color{darkmagenta}d_{\color{darkmagenta}1}\color{darkmagenta}d_{\color{darkmagenta}2}\color{darkmagenta}d_{\color{darkmagenta}3}}\ldots\) satisfy \({\color{darkmagenta}d_{\color{darkmagenta}j}} \in \{0, 1, \ldots , B-1\}\) for all \(j\geq 0\), with the further constraint \({\color{darkmagenta}d_{\color{darkmagenta}0}} \neq 0\) for the leading digit. Again if there are multiple representations we choose the representation where all but a finite number of digits are \(0\) to guarantee uniqueness.

Example 1. In base \(B = 10\) we have

\[1/3 = 3.3333333333333\ldots \times 10^{-1}\]

and

\[1/5 = 2 \times 10^{-1}\]

In base \(B = 2\), we have

\[1/3 = (1.01010101010101010101010101010101010101\ldots )_{2} \times 2^{-2}\]

and

\[1/5 = (1.100110011001100110011001100110011001100\ldots )_{2} \times 2^{-3}\]

Note in particular it depends on the base \(B\) whether a finite significand suffices to represent a rational number.

Example 2. Irrational numbers such as \(\sqrt 2\) or \(\pi\) always require an infinite and aperiodic significand for their representation. In base \(B = 10\) we have

\[\sqrt 2 = 1.4142135623\ldots \times 10^{0}\]

and

\[\pi = 3.1415926535\ldots \times 10^{0}\]

Yet we can equally well use any other base. In base \(B = 2\) we have

\[\sqrt 2 = (1.0110101000001001111001100110011111110011\ldots )_{2} \times 2^{0}\]

and

\[\pi = (1.1001001000011111101101010100010001000010\ldots )_{2} \times 2^{1}\]

Floating point numbers (*)

Now that we understand the basics of the positional number system and the radix point representation, let us return to consider bits and data.

From the perspective of numerical computation, the curse of a fixed-length binary format is that we can allocate only a fixed number of bits to represent an infinity of numbers. Thus, no matter what we do, our computations will not be exact in all cases.

In practice, as standardized in the IEEE 754-2019 standard for floating point arithmetic, a fixed-length format is implemented by

• restricting the significand to a fixed precision \(p\) (number of digits), and

• restricting the exponent \(e\) to a fixed range \(e_\min \leq e \leq e_\max\).

We proceed with a more detailed overview of the binary (\(B = 2\)) representations in IEEE 754-2019. But before we start with the details, it is convenient to have a hands-on example of what floating point numbers look like, on the real line.

Example 1. To give a small but illustrative example, let us assume the binary base \(B = 2\), restrict to \(p = 3\) bits of precision, and restrict the exponent to the range between \(e_\min = -1\) and \(e_\max = 2\). The figure below displays the real line, where we indicate with \(\color{magenta}m\color{magenta}a\color{magenta}g\color{magenta}e\color{magenta}n\color{magenta}t\color{magenta}a\) the so-called “normalized” floating-point numbers and with \(\color{cyan}c\color{cyan}y\color{cyan}a\color{cyan}n\) the so-called “subnormal” numbers with these parameters \(B\), \(p\), \(e_\min\), \(e_\max\). (The precise definitions of the normalized and subnormal numbers are given below.)

Looking at the illustration above, we observe that floating-point numbers “get sparser” the further away we go from zero, with the “subnormal” (cyan) numbers being densest and nearest to zero. Furthermore, floating-point arithmetic is not exact. Say, look at the illustration and suppose we want to compute the sum \(4 + 0.75\). The exact result is of course \(4.75 = (100.11)_{2}\), but from the illustration we see that the closest floating-point number to \(4.75\) is \(5\). Thus, \(4 + 0.75\) will yield the result 5 in floating-point arithmetic with the chosen parameters. (Indeed, representing \(4.75 = (100.11)_2\) exactly would require at least \(p = 5\) bits of precision.)

Example 2. In the example above we wanted to be able to draw every floating point number with the selected parameters on the real line, so we chose rather small parameters. The important point to understand is that qualitatively the same behaviour remains with the actual parameters used in the formats specified by IEEE 754-2019. For example, if we add a large-enough number and a small-enough number, the available precision is not sufficient to take into account the contribution of the small number in the result. Indeed, we can readily witness this at the console:

scala> 1e13 + 0.1
res: Double = 1.00000000000001E13

scala> 1e14 + 0.1
res: Double = 1.000000000000001E14

scala> 1e15 + 0.1
res: Double = 1.0000000000000001E15

scala> 1e16 + 0.1                       // insufficient precision
res: Double = 1.0E16

scala> 1e17 + 0.1                       // insufficient precision
res: Double = 1.0E17

Example 3. Another aspect of floating-point arithmetic that is important to understand is that most implementations of IEEE 754-2019 operate in binary (\(B = 2\)), not in decimal (\(B = 10\)). Thus, what may appear to be innocent in decimal may be somewhat more subtle in binary. Here is a small example to illustrate this at the console:

scala> 0.3 - 0.1
res: Double = 0.19999999999999998

(Recall that you can use the function tellAboutDouble to witness in more detail what happens above. Start by observing at the console that none of \(0.1\), \(0.2\), or \(0.3\) is actually what it appears to be.)

Now that we have a rough intuition what floating-point numbers look like on the real line, let us proceed with the detailed definitions.

Normalized floating-point numbers. A normalized floating point number in base \(B\) is a three-tuple \((s, m, e)\) consisting of

• a sign \(s\in \{0,1\}\),

• a \(p\)-digit significand \(m = ({\color{darkmagenta}d_{\color{darkmagenta}0}}.{\color{darkmagenta}d_{\color{darkmagenta}1}\color{darkmagenta}d_{\color{darkmagenta}2}\color{darkmagenta}d_{\color{darkmagenta}3}}\ldots {\color{darkmagenta}d_{\color{darkmagenta}p\color{darkmagenta}-\color{darkmagenta}1}})_{B}\) with \({\color{darkmagenta}d_{\color{darkmagenta}0}} \neq 0\), and

• an integer exponent \(e\) with \(e_\min \leq e \leq e_\max\).

The number represented by \((s, m, e)\) is

\[(-1)^{s} \times m \times B^{e}\]

Example. As in the illustration above, suppose that \(B = 2\), \(p = 3\), \(e_\min = -1\), and \(e_\max = 2\). The three-tuple \((s, m, e)\) with

\[\begin{split}s &= 0,\\ m &= (1.01)_{2},\\ e &= 1,\end{split}\]

is a normalized floating point number that represents

\[(-1)^{0} \times (1.01)_{2} \times 2^{1} = 1 \times ( 1\times 2^{0} + 0\times 2^{-1} + 1\times 2^{-2}) \times 2^{1} = 2.5\]

Indeed, we see \(2.5\) indicated in magenta in the illustration.

From the definition we observe that a normalized floating point number is always nonzero because the leading digit of the significand is nonzero. To represent very small numbers, and zero in particular, the normalized numbers are extended with subnormal numbers that fix the exponent at \(e = e_\min\) and fix the leading digit of the significand to \({\color{darkmagenta}d_{\color{darkmagenta}0}} = 0\).

Subnormal floating-point numbers. A subnormal floating point number in base \(B\) is a two-tuple \((s, m)\) consisting of

• a sign* \(s \in \{0, 1\}\),

• a \(p\)-digit significand \(m = ({\color{darkmagenta}d_{\color{darkmagenta}0}}.{\color{darkmagenta}d_{\color{darkmagenta}1}\color{darkmagenta}d_{\color{darkmagenta}2}\color{darkmagenta}d_{\color{darkmagenta}3}}\ldots {\color{darkmagenta}d_{\color{darkmagenta}p\color{darkmagenta}-\color{darkmagenta}1}})_{B}\) with \({\color{darkmagenta}d_{\color{darkmagenta}0}} = 0\).

The number represented by \((s, m)\) is

\[(-1)^{s} \times m \times B^{e_\min}\]

Example. As in the illustration above, suppose that \(B = 2\), \(p = 3\), \(e_\min = -1\), and \(e_\max = 2\). The two-tuple \((s, m)\) with

\[\begin{split}s &= 1,\\ m &= (0.01)_{2}\end{split}\]

is a subnormal floating point number that represents

\[(-1)^{1} \times (0.01)_{2} \times 2^{-1} = -1 \times (0\times 2^{0} + 0\times 2^{-1} + 1\times 2^{-2}) \times 2^{-1} = -0.125\]

Indeed, we see \(-0.125\) indicated with cyan in the illustration.

The formats “binary32” and “binary64” in IEEE 754-2019. The two most frequently implemented floating-point formats in IEEE 754-2019 are the format “binary32” (type Float in Scala) and the format “binary64” (type Double in Scala).

The parameters for these formats are:

Format	B	p	emin	emax
binary32	2	24	-126	127
binary64	2	53	-1022	1023

Floating-point arithmetic in IEEE 754-2019. Arithmetic on floating-point numbers is executed according to the following basic rules, subject to the parameters of the format.

• (First, if the input operands are not already floating point numbers, then the floating-point number closest to each input operand is determined. These floating-point numbers become the input operands.)

• Second, the result of the operation on the input operands is computed with infinite precision.

• Third, the closest floating-point number to the infinite-precision result is determined. This floating-point number becomes the result (the output) of the arithmetic operation.

Of course, in practice the second step is not really done with infinite precision, but rather with sufficient (finite) precision to determine the output as if we had actually used infinite precision.

Warning

Caveat. The actual rules in IEEE 754-2019 are slightly more subtle than the simplified version presented above, for example as regards rounding when the closest floating-point number is not unique, and as regards formats in bases other than binary. Always study the actual standard itself in case of doubt.

Example. Let us trace through at the console what happens when we evaluate \(0.3 - 0.1\) in “binary64” (recall the example above). First, let us set up the operands.

scala> val a = 0.3
a: Double = 0.3

scala> val b = 0.1
b: Double = 0.1

Now let us see what the actual “binary64”-format numbers are:

scala> tellAboutDouble(a)
I am a 64-bit word that Scala views as having format 'Double' ...
... my bits are, in binary, (0011111111010011001100110011001100110011001100110011001100110011)_2
... or equivalently, in hexadecimal, 0x3FD3333333333333
... Scala prints me out as 0.3
... indeed, my bits acquire meaning as specified
    in the binary interchange format 'binary64' in the
    IEEE Std 754-2008 IEEE Standard for Floating-Point Arithmetic
    https://dx.doi.org/10.1109%2FIEEESTD.2008.4610935
... this format is a bit-packed format with three components:
                            (0011111111010011001100110011001100110011001100110011001100110011)_2
    a) the sign
       (bit 63):             0
    b) the biased exponent
       (bits 62 to 52):       01111111101
    c) the trailing significand
       (bits 51 to 0):                   0011001100110011001100110011001100110011001100110011
... my biased exponent 1021 indicates that I am a _normalized_ number
    with a leading 1-digit in my significand and
    an unbiased exponent -2 = 1021 - 1023
... that is, in _binary radix point notation_, I am exactly
                                      (1.0011001100110011001100110011001100110011001100110011)_2 * 2^{-2}
... or what is the same in _decimal radix point notation_, I am exactly
    0.299999999999999988897769753748434595763683319091796875

Aha, so what got set up was not \(0.3\) but the closest floating-point number to \(0.3\) in “binary64”, which is

\[\begin{split}\begin{split} (1&.0011001100110011001100110011001100110011001100110011)_{2} \times 2^{-2}\\ &= 0.299999999999999988897769753748434595763683319091796875 \end{split}\end{split}\]

And it is qualitatively the same story with \(0.1\), as we observe:

scala> tellAboutDouble(b)
I am a 64-bit word that Scala views as having format 'Double' ...
... my bits are, in binary, (0011111110111001100110011001100110011001100110011001100110011010)_2
... or equivalently, in hexadecimal, 0x3FB999999999999A
... Scala prints me out as 0.1
... indeed, my bits acquire meaning as specified
    in the binary interchange format 'binary64' in the
    IEEE Std 754-2008 IEEE Standard for Floating-Point Arithmetic
    https://dx.doi.org/10.1109%2FIEEESTD.2008.4610935
... this format is a bit-packed format with three components:
                            (0011111110111001100110011001100110011001100110011001100110011010)_2
    a) the sign
       (bit 63):             0
    b) the biased exponent
       (bits 62 to 52):       01111111011
    c) the trailing significand
       (bits 51 to 0):                   1001100110011001100110011001100110011001100110011010
... my biased exponent 1019 indicates that I am a _normalized_ number
    with a leading 1-digit in my significand and
    an unbiased exponent -4 = 1019 - 1023
... that is, in _binary radix point notation_, I am exactly
                                      (1.1001100110011001100110011001100110011001100110011010)_2 * 2^{-4}
... or what is the same in _decimal radix point notation_, I am exactly
    0.1000000000000000055511151231257827021181583404541015625

So now that we have the actual input operands in “binary64”, let us subtract the two input operands, with infinite precision:

\[\begin{split}\begin{split} 0&.2999999999999999888977697537484345957636833190917968750\\ &-0.1000000000000000055511151231257827021181583404541015625\\ &=0.1999999999999999833466546306226518936455249786376953125 \end{split}\end{split}\]

The closest floating-point number to this infinite-precision result in “binary64” is

\[\begin{split}\begin{split} (1&.1001100110011001100110011001100110011001100110011001)_{2} \times 2^{-3}\\ &= 0.1999999999999999833466546306226518936455249786376953125 \end{split}\end{split}\]

This is of course what Scala reports as well:

scala> val c = a-b
c: Double = 0.19999999999999998

scala> tellAboutDouble(c)
I am a 64-bit word that Scala views as having format 'Double' ...
... my bits are, in binary, (0011111111001001100110011001100110011001100110011001100110011001)_2
... or equivalently, in hexadecimal, 0x3FC9999999999999
... Scala prints me out as 0.19999999999999998
... indeed, my bits acquire meaning as specified
    in the binary interchange format 'binary64' in the
    IEEE Std 754-2008 IEEE Standard for Floating-Point Arithmetic
    https://dx.doi.org/10.1109%2FIEEESTD.2008.4610935
... this format is a bit-packed format with three components:
                            (0011111111001001100110011001100110011001100110011001100110011001)_2
    a) the sign
       (bit 63):             0
    b) the biased exponent
       (bits 62 to 52):       01111111100
    c) the trailing significand
       (bits 51 to 0):                   1001100110011001100110011001100110011001100110011001
... my biased exponent 1020 indicates that I am a _normalized_ number
    with a leading 1-digit in my significand and
    an unbiased exponent -3 = 1020 - 1023
... that is, in _binary radix point notation_, I am exactly
                                      (1.1001100110011001100110011001100110011001100110011001)_2 * 2^{-3}
... or what is the same in _decimal radix point notation_, I am exactly
    0.1999999999999999833466546306226518936455249786376953125

The same basic rule now applies regardless of the arithmetic operation or function that is being evaluated. The result is the floating-point number that is closest to the infinite-precision result, with ties broken as indicated by the current rounding mode.

Consult the standard IEEE 754-2019 for further details.

Warning

Caveat floating-point. The key take-home message from this section is that when you engage in floating-point arithmetic, it is a good idea to know that you are approximating the real numbers with a small finite set of rational numbers, each of which has a finite radix point representation in the selected base. In particular, floating point arithmetic is not exact, loss of precision may occur, and errors may accumulate in the course of a computation. Floating-point arithmetic is a great tool, but it must be used with care.

Arbitrary-precision numbers (**)

The advantage of binary fixed-precision arithmetic is that the arithmetic operations are typically implemented in hardware and hence fast. However, in a number of applications (e.g. public-key cryptosystems such as RSA) such arithmetic does not have sufficient precision. For such purposes, there exist software-based implementations that enable arbitrary-precision arithmetic.

For example, the Scala standard library supports arithmetic with arbitrary-precision integers through class BigInt:

scala> BigInt(2).pow(100)
res2: scala.math.BigInt = 1267650600228229401496703205376
scala> BigInt("10000000000000000000000000",16)     // 2^100 in hexadecimal
res3: scala.math.BigInt = 1267650600228229401496703205376

The Scala standard library supports unscaled arbitrary-precision decimal arithmetic through class BigDecimal, with java.math.mathContext set to UNLIMITED.

Our guided tour of numerical data is now at an end. Next, we will consider textual data.