Textual data (*)

(Excerpt from Adam Smith, An Inquiry into the Nature and Causes of the Wealth of Nations.)

We continue our guided tour by looking at representations of text as a sequence of bits, that is, textual data, and how to manipulate such data in programming terms.

Representing individual characters (*)

The atomic unit for textual data is one character drawn from a character set. A character encoding for a character set specifies a unique numerical (binary) character code for each character in the character set.

Example. Below we display five characters from a character set, and an associated unique 16-bit character code for each character:

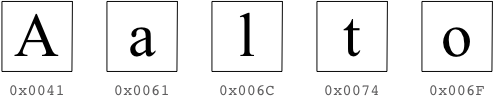
If we concatenate these character codes, we obtain a string, as we can readily witness at the console:

scala> tellAboutString("Aalto")
I am compound data that Scala views as having format 'String' ...
... in essence, I am a sequence of 5 consecutive 16-bit words,
    each of which Scala views as having format 'Char'
... the bits of this sequence are, in binary, (00000000010000010000000001100001000000000110110000000000011101000000000001101111)_2
... or equivalently, in hexadecimal, 0x00410061006C0074006F
... Scala prints me out as Aalto

Character encodings (*)

Many character encodings exist, but every programmer should know the basics of the following two standards

• ASCII (American Standard Code for Information Interchange) for historical reasons, and

• Unicode as the current dominant standard.

ASCII. Let us start by looking at the ASCII code, which is a 7-bit character encoding for specific \(2^7 = 128\) characters. In fact, what we will do is look at the corresponding part of the Unicode standard, namely C0 Controls and Basic Latin, which is exactly the ASCII code when restricted to the least significant 7 bits.

We display the ASCII code in the table below:

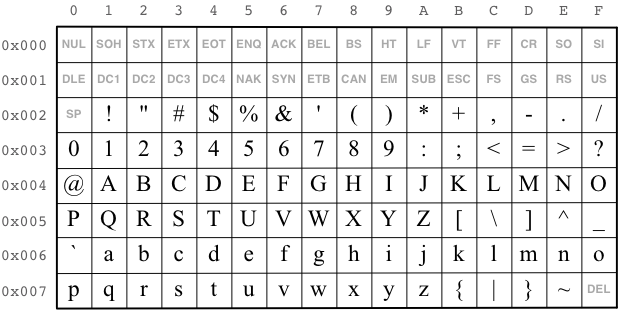
Reading guide for the table. To visually read off character codes of characters from the table, first identify the row index (hexadecimal number) in which the character occurs, and then append the column index as the least significant digit to the number. The ASCII code is the least significant 7 bits of this 16-bit number. (The entire 16-bit number is the character code in the subset of Unicode implemented in Scala.)

Example 1. The ASCII character code for the character 'A' (LATIN CAPITAL LETTER A) is 0x41, or Unicode U+0041.

Example 2. The ASCII character code for the character 'Z' (LATIN CAPITAL LETTER Z) is 0x5A, or Unicode U+005A.

Example 3. The ASCII character code for the character 'a' (LATIN SMALL LETTER A) is 0x61, or Unicode U+0061.

Example 4. The ASCII character code for the character 'z' (LATIN SMALL LETTER Z) is 0x7A, or Unicode U+007A.

Code for empty space. The code 0x20 (SP or SPACE) is special in ASCII. It stands for the empty space ' ' of one character.

Non-printing control codes. Let us return to study the ASCII table above. Observe that table contains many codes such as 0x0D (CR, or CARRIAGE RETURN), 0x0A (LF, or LINE FEED), and 0x09 (HT, or HORIZONTAL TAB) that do not have individual printable characters associated with them. In the early days of computing, these codes were used to control the operation of a teleprinter that would print a stream of ASCII characters to the user. For example, a CARRIAGE RETURN would instruct the terminal device to return the physical printing carriage from its current position back to the first column. Similarly, LINE FEED would advance the paper by one line.

There is one control code in ASCII that every programmer should know. Namely, 0x0A (LINE FEED). In Scala, a LINE FEED is encoded by '\n'. When a line feed is used inside a string, for example in "This is the first line.\nThis is the second line.\n", the line feed character '\n' indicates that the string should be formatted on multiple lines such that each line feed starts a new line. Here is an example:

scala> print("Hello, world!\nOn multiple lines.\n\nHello, again!")
Hello, world!
On multiple lines.

Hello, again!
scala>

Beyond ASCII. ASCII has only 128 character codes, which suffice to capture only a rather limited set of writing systems. Among the systems not captured is, for example, written Finnish, which uses accented scripts such as ‘ä’, ‘ö’, and ‘å’ that are not present in ASCII.

Unicode. Unicode was and is being developed to capture and unify the scripts, symbols, and punctuation used in most writing systems. The current version, Unicode 7.0.0, has a code space from U+0000 to U+10FFFF, that is, there are \(2^{20}+2^{16}=1114112\) codes.

For example, we can find the accented scripts typical to Finnish in the Unicode code range C1 Controls and Latin-1 Supplement (codes U+0080 to U+00FF).

Below we display the Latin-1 Supplement in table format:

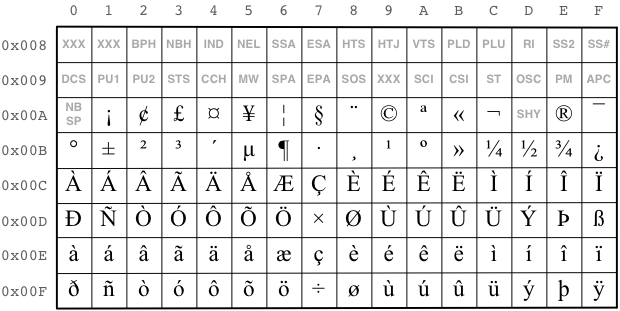
Example 1. The Unicode character code for the character 'Ä' (LATIN CAPITAL LETTER A WITH DIAERESIS) is U+00C4.

Example 2. The Unicode character code for the character 'Å' (LATIN CAPITAL LETTER A WITH RING ABOVE) is U+00C5.

Example 3. The Unicode character code for the character 'Ö' (LATIN CAPITAL LETTER O WITH DIAERESIS) is U+00D6.

Example 4. The Unicode character code for the character 'ä' (LATIN SMALL LETTER A WITH DIAERESIS) is U+00E4.

Example 5. The Unicode character code for the character 'å' (LATIN SMALL LETTER A WITH RING ABOVE) is U+00E5.

Example 6. The Unicode character code for the character 'ö' (LATIN SMALL LETTER O WITH DIAERESIS) is U+00F6.

Unicode in Scala. The value type Char in Scala spans a 16-bit subspace of the entire Unicode space, namely the codes from U+0000 to U+FFFF. The codes from U+0000 to U+007F are exactly the ASCII code when truncated to the least significant 7 bits.

Example. In Scala, you can create characters by writing them literally in single quotes, or with a four-hexadecimal-digit (16-bit) Unicode escape code of the form \uXXXX, where XXXX is replaced with four hexadecimal digits:

scala> val c = 'A'
c: Char = A

scala> c.toShort                  // recall that a Short is a 16-bit word
res: Short = 65

scala> "0x%X".format(c.toShort)
res: String = 0x41

scala> val cc = '\u0041'          // Unicode escape for U+0041 ('A')
cc: Char = A

scala> val ccc = '\u0042'         // Unicode escape for U+0042 ('B')
ccc: Char = B

scala> val cccc = '\u000A'        // Unicode escape for U+000A (line feed)
cccc: Char =


scala>

“Mojibake”, or “ääkkössoppa” (*). Working with textual data, and legacy textual data in particular, may involve conflicts between different character encodings. More often than not, a programmer needs to resolve problems arising from 文字, or Mojibake.

An equivalent in Finnish is that one may observe “ääkkössoppa” in Finnish text, say, “Hääyö” appears as “Hääyö” or “H{{y|”. This is because a legacy character encoding has been used to encode the string as bits, and the current software assumes that the encoding is, say, Unicode serialized using the Unicode transformation format UTF-8. Alternatively it may be that the current software does not support Unicode at all.

Mojibake can typically be cured (at least by filtering out and/or escaping unsupported characters) as soon as the relevant encodings have been identified. Here is a good starting point.

Strings (*)

A string is a sequence of character codes in a character encoding, such as Unicode. Strings have their own type in Scala, type String, to enable working with strings using dedicated methods implemented in StringOps.

Working with strings in Scala. It is a good idea to study what is available in StringOps yourself before attempting to solve the string-related exercises.

Here are some examples to illustrate the possibilities:

scala> "foo".length
res: Int = 3

scala> "foo"(0)
res: Char = f

scala> "foo"(1)
res: Char = o

scala> "foo"(2)
res: Char = o

scala> "foo" ++ "bar"
res: String = foobar

scala> "foobar".capitalize
res: String = Foobar

scala> "foobity bar".take(5)
res: String = foobi

scala> "foobity bar".dropRight(4)
res: String = foobity

scala> "foobity bar".slice(2,6)
res: String = obit

scala> "zum,ba,bum,ba,bum".split(',')
res: Array[String] = Array(zum, ba, bum, ba, bum)

scala> "abcdefghiklm".grouped(3).toArray
res: Array[String] = Array(abc, def, ghi, klm)

scala> "abcdefghiklm".sliding(3).toArray
res: Array[String] = Array(abc, bcd, cde, def, efg, fgh, ghi, hik, ikl, klm)

Formatting strings. A method in StringOps that deserves highlighting is the method format that formats its zero or more arguments into a string as instructed in the format string. Below are some examples how to format data.

Example 1. The most common use of string formatting is to format multiple data items into a single string for purposes of output.

scala> "%s deposits %d euros to %s".format("Jane Doe", 999, "XYZW-123456789ZZ")
res: String = Jane Doe deposits 999 euros to XYZW-123456789ZZ

The format specifiers %s, %d, %s in the string "%s deposits %d euros to %s" indicate how each of the three arguments "Jane Doe", 999, and "XYZW-123456789ZZ" to method format are to be converted into a string.

Example 2. A format specifier may be tailored to format a data item of a given type with careful detail. Suppose we have an Int, and want to format that Int as a string of decimal (base 10) digits, with at least three digits. Furthermore, if less than three digits are available, we want the most significant digits to consist of 0s. After a bit of study, we observe that this can be achieved as follows:

scala> "%03d".format(1)
res: String = 001

scala> "%03d".format(12)
res: String = 012

scala> "%03d".format(123)
res: String = 123

scala> "%03d".format(-123)
res: String = -123

scala> "%03d".format(-1234)
res: String = -1234

Example 3. Suppose we have an Int, and want to format it into hexadecimal format so that the format uses at least 10 characters and is left-justified (right-justified). This can be achieved as follows:

scala> "%-10X".format(1234)
res: String = "4D2       "

scala> "%10X".format(1234)
res: String = "       4D2"

Formatted text (*)

Textual encodings of information are typically semi-structured in the sense that the information is presented in a structured-enough manner to be easily accessible to a program, but not quite as structured as, say, the binary format for a floating-point number where every single bit has a carefully assigned meaning.

Program text written in the Scala programming language is a good example of formatted text. A correctly composed program text has a precise and unequivocal structure and meaning, but we are quite free to interject comments and other decoration such as line breaks or extra space to the text as we like. (Such interjections are more commonly known as white space that the compiler will disregard as it reads the program text.)

Let us however start with easier examples of formatted text.

Tables as text (*)

Information is often represented in the form of a table or relation between attributes. For example, consider the table below:

Name	Age	Eyes	Height	Weight
Alice	23	blue	1.60	50
Bob	25	brown	1.83	72
Joe	50	green	1.75	91
Jill	42	brown	1.71	63

The table has five attributes, “Name”, “Age”, “Eyes”, “Height”, and “Weight”. The table has four information rows (also often called records).

Equally well we could have a set of time-stamped measurements from an array of sensors. In this case time and the sensors consistute the attributes, and each row in the table records the time stamp and the sensor readings.

Time stamp	Sensor1	Sensor2	…	Sensor100
Fri Dec 20 00:00:00.00 EET 2013	0.00	0.00	…	0.00
Fri Dec 20 00:00:00.01 EET 2013	0.00	0.00	…	0.00
Fri Dec 20 00:00:00.02 EET 2013	0.00	0.00	…	0.00
Fri Dec 20 00:00:00.03 EET 2013	0.00	0.00	…	0.00
…	…	…	…	…
Fri Dec 20 23:59:59.98 EET 2013	0.00	0.00	…	0.00
Fri Dec 20 23:59:59.99 EET 2013	0.00	0.00	…	0.00

As programmers we need to be able to manipulate such relational information and transport it across different computer systems and software architectures.

A common solution to implement such transport is to import and export the data as text, since text is easily transported and even manually edited as necessary. Text is also versatile and not bound by specific architectural constraints such as the word length.

Thus it makes sense to format the attributes and records as text, for example so that each record is one line of text, and the attribute values in each line are separated by commas. In many cases it is also convenient to record the names of the attributes as a first line of text, which results in the following textual representation of the table above:

Name,Age,Eyes,Height,Weight
Alice,23,blue,1.60,50
Bob,25,brown,1.83,72
Joe,50,green,1.75,91
Jill,42,brown,1.71,63

CSV. This rather loosely defined practice of representing records as lines of text is called the Comma Separated Values or CSV format. (Of course there is nothing special about the comma “,” as a separator, one could equally well use any other character as the separator and talk about Character Separated Values instead.)

Most programs that operate with tables of records (for example, relational databases, spreadsheet programs, statistical and mathematical software, and so forth) can import and export textual data that represents the records as CSV.

Caveat. CSV is actually a loose family of formats, so in most cases minor tweaking is required (e.g. changing the separator character) for seamless import/export between programs.

Structured objects as text (*)

Beyond simple tables, frequently it is necessary to transport information that has a more heterogeneous and detailed internal structure. That is, we are interested in transporting objects with named attributes and values for those attributes, where a value may in itself be an object, or an array of values. Again a natural approach is to format the objects as text.

JSON. JavaScript Object Notation (JSON) is a widely used textual format for transporting structured objects.

Programs as text – syntax and parsing (**)

Formatted text intended for program consumption must typically adhere to a format – which is in this context typically called a syntax – so that a program can extract the intended information in the text. In the case of programming languages such as Scala that have a rather versatile syntax, the syntax is typically specified by means of a formal grammar, which is used to

• check that the text conforms to the syntax, and

• parse conformant text according to the rules in the grammar.

Remark. Our intent in this round is not to enter into detailed discussion of formal specification of syntax via grammars, and automatic parsing of text conforming to a grammar, but rather to mention in passing that such tools exist to assist a programmer to work with textual data, and these tools will be explored in more detail at subsequent courses. At this point it suffices to know that such tools exist. Nevertheless we will give an illustrative example in the asterisked material below, just in case you are interested.

Context-free grammars (**)

The syntax of many programming languages and other more advanced textual formats can be specified using a class of formal grammars known as context-free grammars. A context-free grammar can be written as a set of rules in Backus–Naur Form (or briefly BNF).

Example. Think about arithmetic expressions consisting of integers (in decimal) combined with the standard arithmetic operations (plus, minus, times, division), possibly grouped with parentheses. Here is a set of rules in BNF (a BNF grammar) that captures the syntax for such arithmetic expressions:

<expression> ::= <integer> |
                 "-" <expression> |
                 "(" <expression> ")" |
                 <expression> "+" <expression> |
                 <expression> "-" <expression> |
                 <expression> "*" <expression> |
                 <expression> "/" <expression>
<integer>    ::= <digit-list>
<digit-list> ::= <digit> |
                 <digit-list> <digit>
<digit>      ::= "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9"

Each rule in the grammar defines a nonterminal (such as <expression>) in the left-hand side of ::= by expressing it as one or more alternative sequences of nonterminals and terminals (such as "+"), where consecutive alternative forms are separated by the vertical bar | symbol. For example, the nonterminal <digit-list> either consists of a single <digit> or a <digit-list> followed by a <digit>. Similarly, an <expression> is either a single <integer> or an operator expression involving one or two subexpressions.

The rules above describe the structure of all arithmetic expressions involving integers, parentheses, and the four standard arithmetic operators. Yet the rules are slightly ambiguous if used in the context of parsing since they do not captured the usual conventions for associativity and precedence of arithmetic operators. For example, we want the expression -5-6-7 to mean \((-5-6)-7 = -18\) and the expression 1+2*3+4 to mean \(1+(2*3)+4=11\), and there is nothing in the grammar above that would give guidance that this is what we want.

The usual associativity and precedence conventions can be captured by introducing more nonterminals in the grammar to remove ambiguity:

<expression> ::= <term> |
                 <expression> "+" <term> |
                 <expression> "-" <term>
<term>       ::= <atom> |
                 <term> "*" <atom> |
                 <term> "/" <atom>
<atom>       ::= <integer> |
                 "-" <atom> |
                 "(" <expression> ")"
<integer>    ::= <digit-list>
<digit-list> ::= <digit> |
                 <digit-list> <digit>
<digit>      ::= "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9"

Suppose now that we have an arithmetic expression such as:

1+2*3+4

The grammar enables us to parse this expression using the rules in the grammar. This results in a parse tree for the expression.

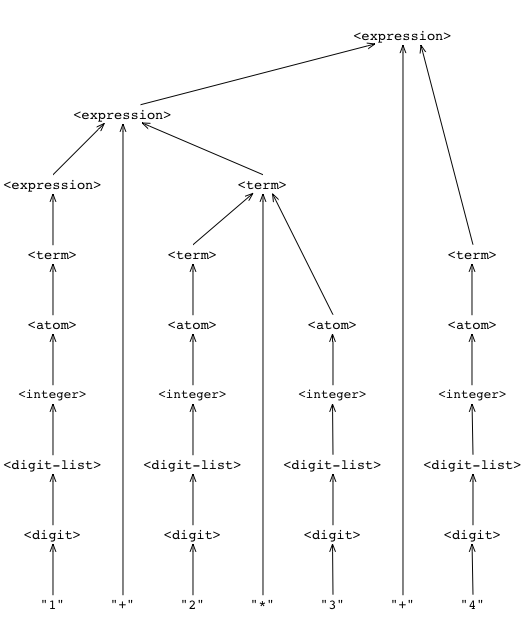
The parse tree in turn enables us to evaluate the expression by attaching an action to each rule in the grammar. For example, proceeding from the bottom up in the parse tree, we first assemble integers from lists of individual digits, then evaluate atoms, terms, and expressions involving those integers, until at the root of the tree we have the value of the expression:

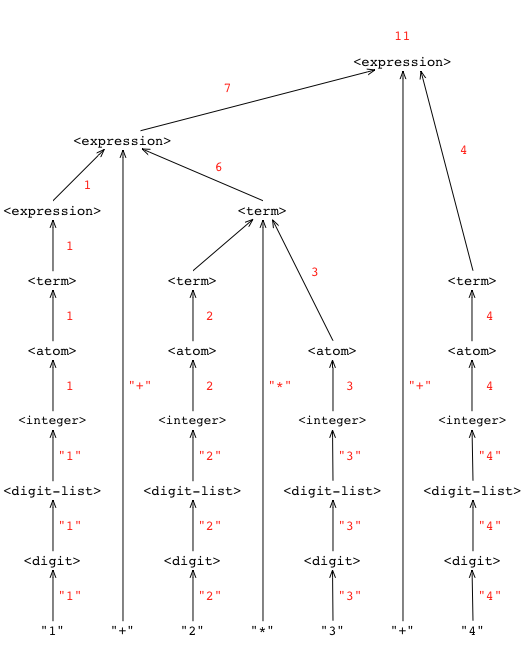
Using the parse tree as a starting point, we can also compile the expression into a more low-level format that can then be executed. This is in fact what the Scala compiler does to Scala program text given to it as input, although the efficient parsing and compilation of Scala program text is a substantially more complex task than the parsing and evaluation of simple arithmetic expressions. Yet, the underlying principles are the same.