Arithmetic with words

Unsigned addition

Recall that our goal for this round is to design a circuit that adds two 64-bit integers. A prerequisite to reach this goal is to understand binary addition. What is it precisely that we must do?

We will focus on unsigned addition, that is, addition of non-negative integers that represent themselves.

Addition in decimal. Before thinking about bits, let us recall some basic arithmetic from our pre-university education. In particular, let us recall the basic algorithm for adding two decimal integers, one decimal digit at a time, proceeding from the least significant digit to the most significant digit, and minding the carry:

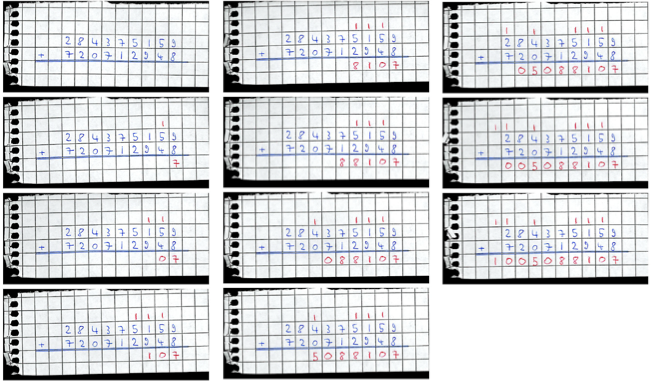
Addition in binary. The algorithm is essentially the same in binary, the only difference is that we are adding binary digits (bits), with the rules

\[\begin{split}0 + 0 &= 0,\\ 0 + 1 &= 1,\\ 1 + 0 &= 1,\\ 1 + 1 &= 10,\end{split}\]

again minding the carry:

In case you happen to be practising your skills at hexadecimal (which you should do – all serious programmers know hexadecimal!), we can easily check the hand calculation above at the console:

scala> val x = 0xAD        //  10101101
x: Int = 173

scala> val y = 0xEB        //  11101011
y: Int = 235

scala> "0x%08X".format(x+y)
res: String = 0x00000198   // 110011000

So now we know what addition looks like at the level of bits.

The ripple-carry adder

So how can we build a 64-bit adder circuit? Let us start by reviewing the specification, that is, what we know about what must be done.

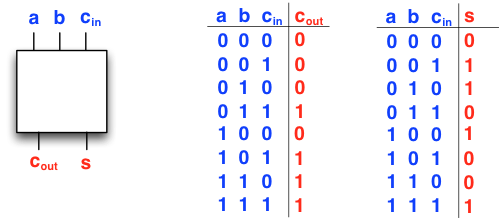
Looking at the examples above, we observe that the basic building block of addition (executed with pen and paper) is the addition of three digits, namely, the carry in from the previous addition (if any), and the two corresponding digits of the summands. The output of such a basic building block is the corresponding digit of the sum, and the carry out (if any). In other words, in binary a complete specification of the building block is:

\[\begin{split}0 + 0 + 0 &= 00\\ 0 + 0 + 1 &= 01\\ 0 + 1 + 0 &= 01\\ 0 + 1 + 1 &= 10\\ 1 + 0 + 0 &= 01\\ 1 + 0 + 1 &= 10\\ 1 + 1 + 0 &= 10\\ 1 + 1 + 1 &= 11\end{split}\]

This leads immediately to a specification for the “basic building block”, an adder that takes three bits as input (or the so-called full adder):

A synthesis is immediate from the truth tables:

def buildFullAdder(a: Gate, b: Gate, c_in: Gate): (Gate, Gate) =
  val c_out = (!a &&  b && c_in)||(a && !b && c_in)||(a && b && !c_in)||(a && b && c_in)
  val s = (!a && !b && c_in)||(!a && b && !c_in)||(a && !b && !c_in)||(a && b && c_in)
  (c_out,s)
end buildFullAdder

We can now cascade the full adders to build the \(n\)-bit ripple-carry adder:

def buildRippleCarryAdder(aa: Bus, bb: Bus) =
  var c: Gate = Gate.False    // no initial carry
  var ss = new Array[Gate](aa.length)
  for i <- 0 until aa.length do
    val cs = buildFullAdder(aa(i),bb(i),c)
    c = cs._1      // carry from bit i propagates to bit i+1
    ss(i) = cs._2
  end for
  new Bus(ss.toSeq) // Make array to Seq and construct Bus
end buildRippleCarryAdder

val n = 4
val aa = Bus.inputs(n)
val bb = Bus.inputs(n)
val ss = buildRippleCarryAdder(aa, bb)

val t = new Toggler()
t.watch("aa", aa.reverse)
t.watch("bb", bb.reverse)
t.watch("ss", ss.reverse)
t.go()

This design is perhaps best illustrated by drawing the circuit for \(n = 4\) with “boxes” illustrating the full adders built in each iteration \(i = 0,1,2,3\):

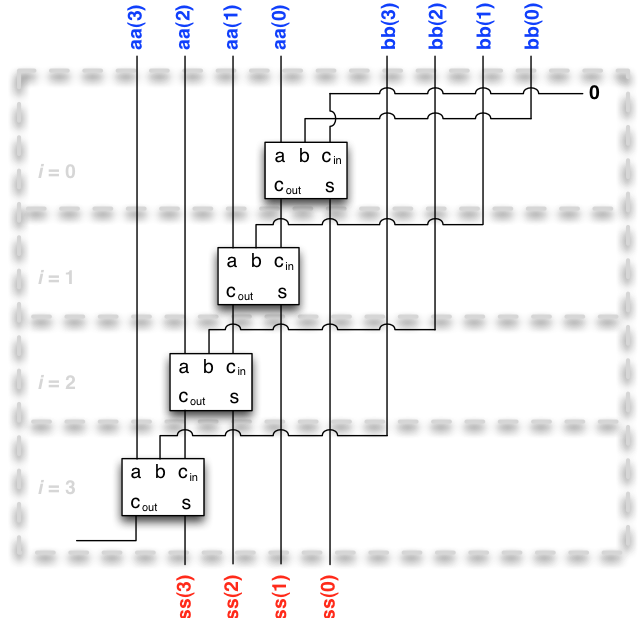
Observe how the circuit reflects precisely the procedure that we used to add numbers manually, one digit at a time, with the carry bit propagating from one adder to the next.

Here is the same design but implemented via the scanLeft operation and a case-construct to decompose the input:

def buildRippleCarryAdder(aa: Bus, bb: Bus) =
  new Bus(
   ((aa zip bb).scanLeft((Gate.False, Gate.False))) {
     case ((c,s),(a,b)) => buildFullAdder(a,b,c)
  }.drop(1).map(_._2))
end buildRippleCarryAdder

Again we have encapsulated the circuit construction into a builder function, so we can abstract away the implementation. We simply have a “white box” that takes two \(n\)-bit-wide buses as inputs, and outputs an \(n\)-bit-wide bus:

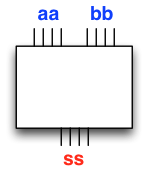
Now take \(n=64\) to reach our goal for this round.

Yet again we can increase the complexity of our designs to use the new builder as a basic building block. Indeed, in the exercises you are invited to build a multiplier circuit by relying on adder circuits. (Furthermore, many of the circuits that we have already built or will build in the exercises will be used as basic building blocks in Round 4: Sequential logic, state and feedback.)

Unsigned multiplication

Also in the context of multiplication we have a fair amount of pre-university education, so many of us recall at least one algorithm how to multiply in decimal. (There are considerably faster ways to multiply large integers than the “classical” algorithm, both in theory and in practice; however, these need not concern us now.)

Multiplication in decimal. In the classical algorithm, we take one operand, say, the left (top) operand, and multiply it with each digit of the right (bottom) operand in turn, recalling to left-shift the result of the multiplication so that the least significant digit of the result aligns with the digit of the right operand being considered:

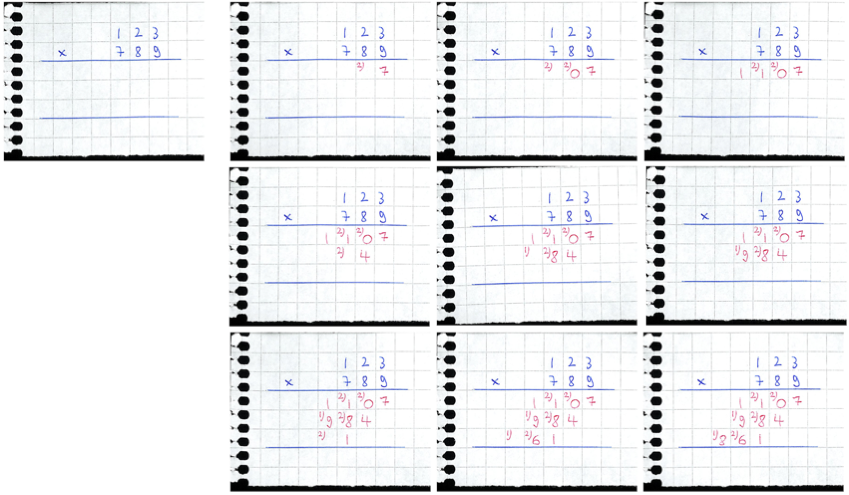
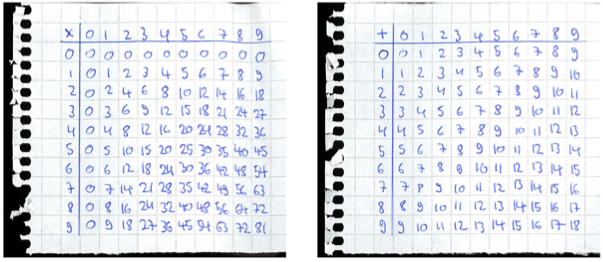
As we recall and/or observe, for fast execution of this procedure on cerebral hardware, one is required to subroutinize digit-by-digit decimal multiplication (in most cases, in the form of a multiplication table). One also has to mind the carry when adding up the results of the digit-by-digit multiplications, so a subroutinized digit-by-digit addition table is useful too:

Finally, we add up the results, again minding the carry:

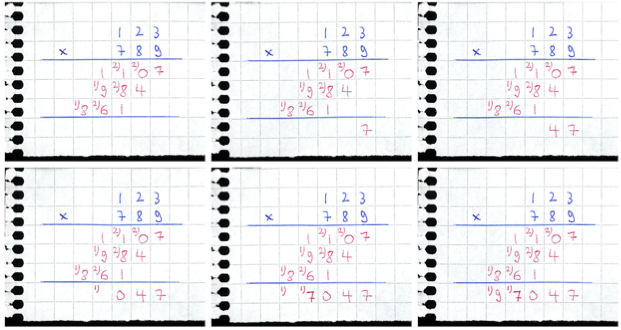
In fact, the proper implementation is to accumulate the final sum with repeated invocations of the classical addition algorithm:

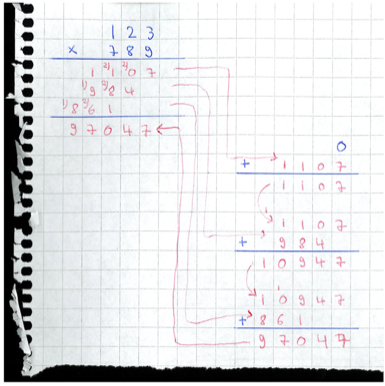
Or what is the same in Scala, with 32 bits of precision:

scala> 123*789
res: Int = 97047

Multiplication in binary. In binary, multiplication becomes procedurally easier. For each 1-bit in the right (bottom) operand, we take a copy of the left (top) operand (appropriately left-shifted), and accumulate the results with binary addition:

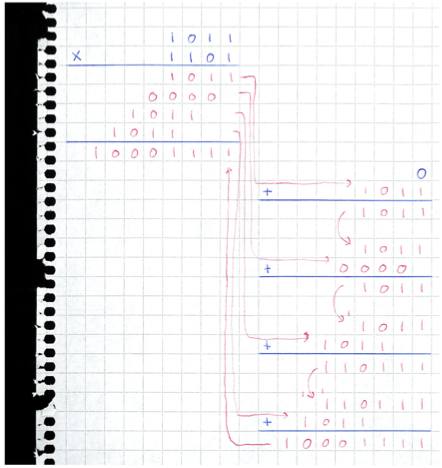
Observe that this is the same algorithm as in decimal, but our multiplication and addition tables now have size \(2\times 2\):

In particular, there is no carry in bit-by-bit multiplication, which simplifies the procedure considerably – all that is needed is left-shifting and addition. Accordingly, binary multiplication is more straightforward to implement in non-cerebral hardware.

And of course we can witness the same in Scala, with 32 bits of precision:

scala> val x = 0xB           //     1011
x: Int = 11

scala> val y = 0xD           //     1101
y: Int = 13

scala> "0x%08X".format(x*y)
res: String = 0x0000008F     // 10001111

Fixed-length arithmetic and overflows (*)

Recall that the word length of a computer architecture is the available precision in bits that is implemented and hence fixed in hardware.

When an arithmetic operation is executed on two fixed-precision operands (in any base, say decimal or binary), the result of the operation may overflow the available fixed precision. To see that this may happen, observe that in the examples above, the result in general has more bits (digits) than the two operands.

Note

Fact. The sum of two non-negative \(b\)-bit operands requires up to \(b+1\) bits of precision, and the product of two non-negative \(b\)-bit operands requires up to \(2b\) bits of precision.

There are two basic approaches for dealing with overflow:

• Truncation retains only the least significant bits (or digits) up to the word length, and disregards the overflowing more significant bits. If you are familiar with modular arithmetic, truncation corresponds to arithmetic modulo \(2^b\), where \(b\) is the word length.

• Storing retains both the least significant bits of the result, up to the word length, and the overflow, if any. In case of addition, the overflow is stored into an auxiliary carry bit. In case of multiplication, the overflow is stored into an auxiliary word (for example, into a dedicated processor register that receives the overflow).

Scala implements truncating arithmetic, even if in many cases the underlying hardware would actually support arithmetic that stores the overflow.

In Scala we can observe that Int truncates to 32 bits by engaging in arithmetic where the result requires more than 32 bits of precision, in which case truncation happens:

scala> 0xFFFFFFFF+0x00000001
res: Int = 0                  // 0x100000000 is truncated to 0x00000000

scala> 0x10000*0x10000
res: Int = 0                  // 0x100000000 is truncated to 0x00000000

scala> 0x10001*0x10000
res: Int = 65536              // 0x100010000 is truncated to 0x00010000

Indeed, if we increase precision to 64 bits (Long), we obtain the correct (that is, non-truncated) result:

scala> 0x00000001L+0xFFFFFFFFL
res: Long = 4294967296        // 0x100000000L

scala> 0x10000L*0x10000L
res: Long = 4294967296        // 0x100000000L

scala> 0x10001L*0x10000
res: Long = 4295032832        // 0x100010000L

Truncation might look like a curse from hardware, but in fact it presents a mixed blessing for signed arithmetic.

Signed integers (*)

This section may be safely skipped, but readers interested in the binary representation of signed integers (for example, the inner workings of the value types Byte, Short, Int, and Long in Scala) or wanting a payoff of their studies at modular arithmetic should pay attention.

So far we have considered only non-negative (unsigned) integers in binary. Let us now proceed to represent signed integers in binary, that is, integers that may be positive or negative (or zero).

There are many ways to represent negative integers in fixed-precision arithmetic. (See here.) Perhaps the most common representation is the two’s complement representation, which is also the representation that Scala uses internally.

To develop two’s complement representation, it is perhaps best to start with something that is more familiar. In particular, we again consider first the decimal system and only then proceed to the binary system. In the case of decimals we speak of ten’s complement representation since the base is 10.

Suppose we have, say, six decimal digits of precision available to represent integers. That is, we can represent the (unsigned) integers \(0, 1, \ldots, 999999\).

The gist of ten’s complement representation is that some of these unsigned integers will actually represent negative integers. Or more bluntly and concretely, even if we actually see \(999999\), we report to the user that we see \(-1\). And, making a very brief digression to binary, it would appear that Scala is also engaging in something that looks like the binary equivalent of what we just outlined (!):

scala> val x = 0xFFFFFFFF  // no minus sign over here ...
x: Int = -1                // ... and yet a -1 ... !?!

Now back to base 10 again. With six digits of precision, we will have the unsigned integers \(500000, 500001, \ldots, 999999\) represent the negative integers \(-500000, -499999, \ldots, -1\), in this order of correspondence.

Let us now develop the intuition that will reveal why this representation is useful. Let us assume that our arithmetic is truncating. That is, since we have six digits of precision, we only retain the six least significant digits of the result of any arithmetic operation, even if the result has more digits. Say, if the result is \(1000000\), we truncate it to \(0\), and if the result is \(1000123\), we truncate it to \(123\).

So far so good. Let us now think carefully about how to select representatives for negative numbers. Say, suppose we need to represent the negative number \(-1\). Which of the possibilities \(0, 1, \ldots, 999999\) would be a natural representative for the negative number \(-1\) ?

Let us think about this a bit. Say, it would be a nice property if we could add positive and negative integers so that the result would be intuitive. For example, we would like that \(1 + (-1) = 0\). How would we achieve this with truncation? Which of the integers \(0, 1, \ldots, 999999\) should be the representative of \(-1\)?

After a little bit of thought, let us pick \(999999\) as the representative of \(-1\). In this case we have \(1 + 999999 = 1000000\), and the latter truncates to \(0\). Thus, \(1 + (-1) = 0\) holds for this choice, and thus we appear to be pursuing something fruitful. To further strengthen our intuition that we are onto something, it makes sense to represent \(-2\) by \(999998\), \(-3\) by \(999997\), \(-4\) by \(999996\), and so forth. Indeed, suppose we want to compute \(5+(-3)\). Recalling that the representative of \(-3\) is \(999997\), we compute \(5+999997=1000002\), which is \(2\) after truncation, which makes perfect sense. Similarly, suppose we want to compute \(3+(-5)\). Recalling that the representative of \(-5\) is \(999995\), we compute \(3+999995=999998\), which is exactly the representative of \(-2\). Thus, it makes perfect sense to represent negative integers in this way. In particular, we can work with negative integers by encoding them as unsigned integers, and relying on unsigned arithmetic only.

So how should we balance the unsigned integers between representations of positive and negative integers? An established convention is to have the first half of the unsigned integers in \(0, 1, \ldots 999999\), namely \(0, 1, \ldots, 499999\) represent themselves, and have the other half, namely, \(500000, 500001, \ldots, 999999\) represent the negative integers \(-500000, -499999, \ldots, -1\). (Note that the choice is not completely balanced between positive and negative integers since \(-500000\) is represented but \(500000\) is not, in particular because we chose that \(0\) represents itself, so there is one less positive integer available.)

In general terms, suppose we have \(d\) digits of precision and are working in base \(B\). (In the motivating discussion above, \(d = 6\) and \(B = 10\).)

Note

Definition. Assuming we are working with \(d\) digits of precision, the \(B\)’s complement representation for signed integers is as follows:

• each unsigned integer \(z\) with \(0 \leq z \leq B^{d}/2-1\) represents itself, and

• each unsigned integer \(z\) with \(B^{d}/2 \leq z \leq B^{d}-1\) represents the negative integer \(z-B^d\).

In particular, two’s complement representation for signed binary integers with \(b\) bits of precision is obtained by taking \(B = 2\) and \(d = b\).

Example 1. Let us assume \(d = 6\) digits of precision and base \(B = 10\). Then,

• the ten’s complement representation for the signed integer \(-5\) is the unsigned integer \(999995\),

• in ten’s complement representation, the unsigned integer \(999995\) represents the signed integer \(-5\),

• the ten’s complement representation for the signed integer \(123\) is the unsigned integer \(123\), and

• in ten’s complement representation, the unsigned integer \(123\) represents itself, namely the signed integer \(123\).

Example 2. Let us assume \(b = 8\) bits of precision and base \(B = 2\). Then,

• the two’s complement representation for the signed integer \(-(10001)_2\) is the unsigned integer \((11101111)_2\),

• in two’s complement representation, the unsigned integer \((11101111)_2\) represents the signed integer \(-(10001)_2\),

• the two’s complement representation for the signed integer \((1101)_2\) is the unsigned integer \((1101)_2\), and

• in two’s complement representation, the unsigned integer \((1101)_2\) represents itself, namely the signed integer \((1101)_2\).

All right, so that was the general definition, followed by some examples. But how do we negate integers in practice, say, in two’s complement? That is, given \(z\) as input in \(B\)’s complement representation, how do we determine the \(B\)’s complement representation of \(-z\), that is, how do we negate \(z\) in \(B\)’s complement representation? (Note that addition and negation suffice for subtraction, because \(y-z = y+(-z)\).)

Note

Definition. Assuming we are working with \(d\) digits of precision, the \(B\)’s complement of the integer \(0 \leq z \leq B^{d}-1\) is the integer \(B^{d}-z\), truncated to d digits of precision.

That was the definition, but we should still be somewhat annoyed since the definition did not make it particularly easy to negate a number. Computing \(B^{d}-z\), say, \(1000000-z\) in decimal with six digits of precision is still laborious, since the subtraction may require borrowing. And the same holds in binary – say, computing \((100000000)_{2}-(10001)_{2}=(11101111)_{2}\) (at least by hand calculation) is simply annoying. So is there anything we can do?

Let us think about this. Again forget about binary for now. Let us work in base \(B = 10\) and with six digits of precision. We know that \(1000000-z\) is annoying to compute with all the borrowing, so, say, what if we computed \(999999-z\) instead, with \(0 \leq z \leq 999999\)? Would there be any borrowing when we carry out the subtraction?

If you think about it, you will see that there is no need to borrow, since every digit of \(z\) is in the range from \(0\) to \(9\), so when subtracting from \(999999\) there will be no need to borrow. Thus computing \(999999-z\) is straightforward, even by hand calculation. We just subtract each digit in turn, independently of the other digits!

This observation generalizes to an arbitrary base and precision:

Note

Definition. Assuming we are working with \(d\) digits of precision, the \((B-1)\) s’ complement of the integer \(0 \leq z \leq B^{d}-1\) is the integer \(B^{d}-1-z\).

In particular, in the binary case \(B = 2\) determining the ones’ complement is an effortless operation both for humans and machines: we simply complement each bit in turn, up to the number of bits of precision. Say, the ones’ complement of \((10001)_{2}\) with \(b = 8\) bits of precision is \((11101110)_{2}\). Or equivalently, \((11111111)_{2}-(10001)_{2}=(11101110)_{2}\). There is no need to borrow, we just complement each bit in turn, independently of the other bits, up to the number of bits of precision.

Comparing the two previous definitions, we see that \((B-1)\) s’ complement (which is easy to compute) and \(B\) ‘s complement are related. Namely, the latter can be obtained from the former by adding one (and truncating to \(d\) digits of precision).

Example 1. Working in base \(B = 10\), let us work out the ten’s complement of \(123456\) with eleven digits of precision. First, we compute the nines’ complement of \(123456\) with eleven digits of precision, which is \(99999876543\). Then we add one to the result (and truncate if necessary), to get \(99999876544\).

Example 2. Working in base \(B = 2\), let us work out the two’s complement of \((111000)_{2}\) with eleven bits of precision. First, we compute the ones’ complement of \((111000)_{2}\) with eleven digits of precision, which is \((11111000111)_{2}\). Then we add one to the result (and truncate if necessary), to get \((11111001000)_{2}\).

So now we know how to effortlessly negate integers in \(B\)’s complement representation. Let us put this skill into use by showing how to engage in signed arithmetic using only unsigned addition.

Example 1. Let us work in base \(B = 10\) with eight digits of precision. Suppose we must compute \(12345-496732\). Let us compute \(12345+(-496732)\) in ten’s complement representation and analyse the result. First, we need ten’s complement representation of both \(12345\) and \(-496732\) with eight digits of precision. It is immediate that \(12345\) represents itself. We can determine the representation of \(-496732\) by negating \(496732\) in ten’s complement. First, the nines’ complement of \(496732\) with eight digits of precision is \(99503267\). Thus, the two’s complement of \(496732\) is obtained by adding one to the result (and truncating if necessary), which yields \(99503268\). Now let us make the unsigned addition \(12345 + 99503268\) to obtain \(12345 + 99503268 = 99515613\). We observe that the result has eight digits, and the most significant digit is greater than \(4\). Thus, we find that the result is the two’s complement representation of a negative number. Let us negate \(99515613\) in ten’s complement to find out the absolute value result. The nines’ complement is \(484386\), and hence ten’s complement is \(484387\). The result of \(12345-496732\) is thus \(-484387\).

Example 2. Let us work in base \(B = 2\) with ten bits of precision. Suppose we must compute \((101011101)_{2}-(10101101)_{2}\). Let us compute \((101011101)_{2}+(-(10101101)_{2})\) in two’s complement representation and analyse the result. First, we need two’s complement representation of both \((101011101)_{2}\) and \(-(10101101)_{2}\) with ten bits of precision. It is immediate that \((101011101)_{2}\) represents itself. We can determine the representation of \(-(10101101)_{2}\) by negating \((10101101)_{2}\) in two’s complement. First, the ones’ complement of \((10101101)_{2}\) with ten bits of precision is \((1101010010)_{2}\). Thus, the two’s complement of \((10101101)_{2}\) is obtained by adding one to the result (and truncating if necessary), which yields \((1101010011)_{2}\). Now let us make the unsigned binary addition \((101011101)_{2} + (1101010011)_{2}\) to obtain \((101011101)_{2} + (1101010011)_{2} = (10010110000)_{2}\). Truncating to ten bits, we have \((10110000)_{2}\). We observe that the result has fewer than ten bits, so the result is a positive number in two’s complement representation. That is, the result of \((101011101)_{2}-(10101101)_{2}\) is \((10110000)_{2}\).

All right. So why does the \(B\)’s complement representation work, mathematically, and enable us to work with unsigned additions only to carry out signed arithmetic with negations and subtractions?

If you are familiar with modular arithmetic, to justify \(B\)’s complement representation it suffices to observe that

\[-y \equiv B^{d}-y \pmod{B^{d}}.\]

That is, the negation \(-y\) of an integer \(y\) is equivalent modulo \(B^{d}\) (that is, truncated to \(d\) digits of precision in base \(B\)) to the integer \(B^{d}-y\).

We can readily test that Scala implements 32-bit two’s complement representation for type Int:

scala> 0x80000000
res: Int = -2147483648

scala> 0xFFFFFFFF      // all 1s in binary is -1 in two's complement
res: Int = -1

scala> 0xFFFFFFFF+2
res: Int = 1

Indeed, all the basic value types Byte, Short, Int, Long are signed types that implement two’s complement representation. In particular, comparisons between elements are signed comparisons, as we can readily test:

scala> 0xFFFFFFFF < 0             // -1 < 0
res: Boolean = true

scala> 0xFFFFFFFF < 0x7FFFFFFF    // -1 < 2147483647
res: Boolean = true

scala> 0xFFFFFFFF < 0x80000000    // -1 < -2147483648
res: Boolean = false

In Scala, the ones’ complement operation is available via the (equivalent) bitwise NOT operator “~”. We witness that integer negation in Scala (two’s complement) is exactly ones’ complement plus one:

scala> val x = 123456     // 0x0001E240
x: Int = 123456

scala> -x == ~x+1
res: Boolean = true

scala> -x
res: Int = -123456        // 0xFFFE1DC0

scala> ~x
res: Int = -123457        // 0xFFFE12BF