Bus-level design
Customizing Scala collections
Now that we have data and control put into good use, let us approach the next issue in terms of design convenience. Namely, the transition from designing with individual wires that carry bits (that is, individual gates in our Scala simulation) to designing with buses of wires that carry words (that is, sequences of gates in our Scala simulation). Recall from Round 2: Bits and data that a word is the atomic unit by which a processor architecture manipulates data. The word length of the architecture is the number of bits in a word.
The necessity to design at the level of words is of course an excellent motivation to drill into the Scala collections framework, and in particular into the tools to manipulate sequences. If possible, we want our bus-level designs to be just as succinct as our gate-level designs. Indeed, recall that our goal for this round is to build a Boolean circuit that adds two 64-bit integers.
Let us start by recalling our gate-level design for selecting between two gates:
val r = (a && !s) || (b && s)
Here a and b were the data inputs (individual gates), and s was the control input (individual gate).
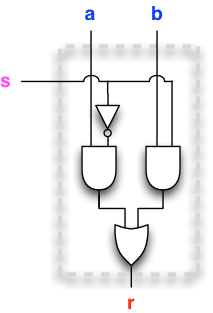
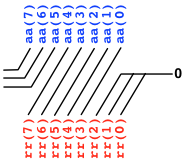
We want to upgrade the gate-selector to a bus-selector, that selects between two n-bit buses. Here we display a bus-selector that selects between two 4-bit buses, aa and bb, to produce the 4-bit bus rr as output.
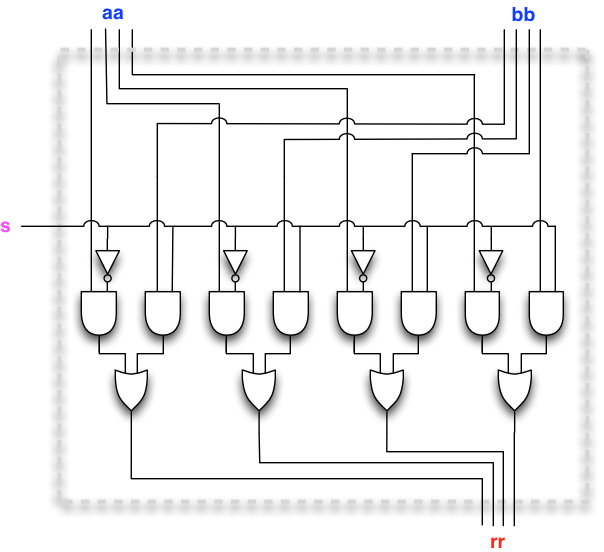
The circuit diagram may look a bit daunting at first, but observe that this is in fact not the case. The same two-input selector is simply repeated four times, once for each pair of corresponding bits aa(i) and bb(i) in the two buses. In particular, the same control input s drives all four selectors.
To enter the realm of bus-level design, let us first try to work with the obvious
abstraction, namely let us just work with an array of gates Array[Gate]
whenever a bus is needed.
Say, let us transport the gate-level design into a design with two n-bit buses with n = 4. Let us build these buses out of input elements:
val n = 4
val aa = new Array[Gate](n)
for i <- 0 until n do aa(i) = new InputElement()
val bb = new Array[Gate](n)
for i <- 0 until n do bb(i) = new InputElement()
val s = new InputElement()
Here is a first attempt to build a two-bus selector that uses
a for-loop over the bits of the bus:
val rr_attempt1 = new Array[Gate](n)
for i <- 0 until n do
rr_attempt1(i) = (aa(i) && !s)||(bb(i) && s)
end for
This code will build precisely the circuit depicted above, so in principle we are done.
But again we should be more critical. Indeed, we are using a for-loop
when far more succinct and idiomatic expressions exist for the task.
Also the need to reserve new Array-objects looks cumbersome.
Here are three further attempts, throwing in some skill at using Scala collections and anonymous functions. (Do not worry if you cannot follow in detail what these one-liners do, we will get practice during later rounds.) Here we go:
val rr_attempt2 = (aa.map(_ && !s) zip bb.map(_ && s)).map((p,q) => p || q)
Here is another go:
val rr_attempt3 = (aa zip bb).map((a,b) => (a && !s) || (b && s))
And yet another:
val rr_attempt4 = (aa zip bb).map(x => (x._1 && !s) || (x._2 && s))
A quick Toggler session gives us a fair amount of confidence that
all four solutions work (try this!):
val t = new Toggler()
t.watch("aa", aa)
t.watch("bb", bb)
t.watch("s", s)
t.watch("rr1", rr_attempt1)
t.watch("rr2", rr_attempt2)
t.watch("rr3", rr_attempt3)
t.watch("rr4", rr_attempt4)
t.go()
Several working solutions are a fair start, but we should not be happy, since the Scala code is far from succinct and readable.
So what is it that we would like? An appropriately apt solution would perhaps be:
val rr = (aa && !s)|(bb && s)
And while we are at it, perhaps the setup code could be also cleaned. If we place some routine setup code into aptly named companion objects, the entire two-bus selector gets built with:
val n = 4
val aa = Bus.inputs(n)
val bb = Bus.inputs(n)
val s = Gate.input()
val rr = (aa && !s)|(bb && s)
Incidentally, the bus-level design tools are already implemented
in package tinylog. Just copy and paste what is above into your
console after include tinylog.* to witness this.
The package tinylog is included with the exercises for this round. If you open it up you will see something like in the listing below. Understanding the entire code is not necessary at this point, but note that Bus extends Seq[Gate], that is, a bus is a sequence of Gate objects. This allows us to perform standard sequence operations, such as zip on Bus as well as the defined custom methods.
package tinylog
import scala.collection.{SpecificIterableFactory, StrictOptimizedSeqOps, mutable}
import collection.SeqOps
sealed class Bus(gates: Seq[Gate]) extends Seq[Gate]
with SeqOps[Gate, Seq, Bus]
with StrictOptimizedSeqOps[Gate, Seq, Bus]:
// Mandatory implementation of `apply` in SeqOps
def apply(idx: Int) = gates.apply(idx)
/** Creates a new Bus from a set of indexes to this one.*/
def apply(idxs: Seq[Int]) = new Bus(idxs.map(gates(_)))
// Mandatory implementation of `length` and `iterator`
def length = gates.length
def iterator = gates.iterator
/* Operations on Gates.*/
/** Values of Gates.*/
def values = gates.map(_.value)
/** The number of gates (i) in this bus and (ii) recursively referenced by the ones in this bus. */
def nofGates: Int =
val counted = new mutable.HashSet[Gate]()
gates.foldLeft(0)((result, gate) => result + gate.nofReferenced(counted))
/**
* For a bus aa and gate g, aa && g returns a new bus cc
* of length aa.length such that cc(i) is aa(i) && g.
*/
def &&(that: Gate) = new Bus(this.map(_ && that))
/**
* For a bus aa and gate g, aa || g returns a new bus cc
* of length aa.length such that cc(i) is aa(i) || g.
*/
def ||(that: Gate) = new Bus(this.map(_ || that))
/**
* Bitwise negation of the bus.
* For a bus aa, ~aa is a new bus cc such that cc(i) is !aa(i).
*/
def unary_~ = this.map(!_)
/**
* Bitwise AND of two busses.
* For two busses aa and bb, aa & bb returns a new bus cc
* of length aa.length such that cc(i) is aa(i) && bb(i).
* The busses must be of the same length.
*/
def &(that: Bus) =
require(this.length == that.length, "Cannot take bitwise and of busses of different length")
new Bus((this zip that).map(x => x._1 && x._2))
/**
* Bitwise OR of two busses.
* For two busses aa and bb, aa | bb returns a new bus cc
* of length aa.length such that cc(i) is aa(i) || bb(i).
* The busses must be of the same length.
*/
def |(that: Bus) =
require(this.length == that.length, "Cannot take bitwise and of busses of different length")
new Bus((this zip that).map(x => x._1 || x._2))
/* Because Bus is a custom collection (based on Seq) with SeqOps trait
we need to override a a few methods so that it can inherit all of the
standard operations from the trait while still behaving as a Bus as
much as possible.
If you are interested, see the RNA exampe at
https://docs.scala-lang.org/overviews/core/custom-collections.html#final-version-of-rna-strands-class
*/
// Mandatory overrides of `fromSpecific`, `newSpecificBuilder`,
// and `empty`, from `IterableOps`
override protected def fromSpecific(coll: IterableOnce[Gate]): Bus =
Bus.fromSpecific(coll)
override protected def newSpecificBuilder: mutable.Builder[Gate, Bus] =
Bus.newBuilder
override def empty: Bus = Bus.empty
// Overloading of `appended`, `prepended`, `appendedAll`, `prependedAll`,
// `map`, `flatMap` and `concat` to return a `Bus` when possible
def concat(suffix: IterableOnce[Gate]): Bus =
strictOptimizedConcat(suffix, newSpecificBuilder)
@inline final def ++ (suffix: IterableOnce[Gate]): Bus = concat(suffix)
def appended(base: Gate): Bus =
(newSpecificBuilder ++= this += base).result()
def appendedAll(suffix: Iterable[Gate]): Bus =
strictOptimizedConcat(suffix, newSpecificBuilder)
def prepended(base: Gate): Bus =
(newSpecificBuilder += base ++= this).result()
def prependedAll(prefix: Iterable[Gate]): Bus =
(newSpecificBuilder ++= prefix ++= this).result()
def map(f: Gate => Gate): Bus =
strictOptimizedMap(newSpecificBuilder, f)
def flatMap(f: Gate => IterableOnce[Gate]): Bus =
strictOptimizedFlatMap(newSpecificBuilder, f)
// The class name will by default be shown as 'Seq', we don't want that.
override def className = "Bus"
object Bus extends SpecificIterableFactory[Gate, Bus]:
def empty: Bus = new Bus(Seq.empty)
def newBuilder: mutable.Builder[Gate,Bus] =
mutable.ArrayBuffer.newBuilder[Gate]
.mapResult(s=>new Bus(s.toSeq))
def fromSpecific(it: IterableOnce[Gate]): Bus = it match
case seq: Seq[Gate] => new Bus(seq)
case _ => new Bus(it.iterator.toSeq)
/** Returns a new bus with n InputElement gates */
def inputs(n: Int) = new Bus((1 to n).map(x => Gate.input()))
/** Returns a new bus of n False gates */
def falses(n: Int) = new Bus((1 to n).map(x => Gate.False))
/** Returns a new bus of n True gates */
def trues(n: Int) = new Bus((1 to n).map(x => Gate.True))
What sets a Bus apart from a plain sequence of objects of type Gate is that there are custom methods
(operator definitions) inside class Bus that enable succinct bus-level
building:
def &&(that: Gate) = new Bus(this.map(_ && that))
def ||(that: Gate) = new Bus(this.map(_ || that))
def unary_~ = this.map(!_)
def &(that: Bus) = new Bus((this zip that).map(x => x._1 && x._2))
def |(that: Bus) = new Bus((this zip that).map(x => x._1 || x._2))
Let us take a more detailed look at these operators. (At this point it may be convenient to recall how we defined the gate-level operators in the previous section.)
First, let us look at the operators
def &&(that: Gate) = new Bus(this.map(_ && that))
def ||(that: Gate) = new Bus(this.map(_ || that))
Observe that the operators && and || are defined so that the
left operand (this) is a Bus, and the right operand (that)
is a Gate. In both cases the result is a new bus, consisting of AND and
OR gates (depending on whether && or || was applied) such that the left
input is a gate from the bus, and the right input
is the right operand (the gate that). (The expression _ && that
is a shorthand for the function z => z && that.)
If you are familiar with vectors and scalars, this is the circuit-building
analogue of operating on a vector with a scalar.
The following figure illustrates the bus that gets
built when we execute the expression
bb && g for a 4-gate bus bb and a gate g.
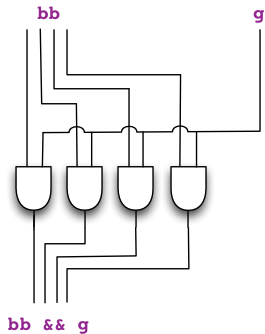
Let us proceed to the next operator:
def unary_~ = this.map(!_)
The operator ~ builds, one entry of its operand (this) at a time,
a NOT-gate that takes input from the entry (the gate of the bus),
and returns a bus consisting of the NOT-gates built.
This is, in essence, the circuit-building analogue of vector negation.
The following figure illustrates the bus that gets
built when we execute the expression ~bb
for a 4-gate bus bb.
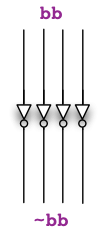
Let us then look at the remaining operators:
def &(that: Bus) = new Bus((this zip that).map(x => x._1 && x._2))
def |(that: Bus) = new Bus((this zip that).map(x => x._1 || x._2))
In this case both operands (this and that) are buses.
The operator & (respectively, the operator |) builds,
one entry at a time, an AND-gate (OR-gate) that takes input from the
corresponding entries (gates) in the left and right operands, and
return a bus consisting of the AND-gates (OR-gates) built.
This is the circuit-building analogue of vector addition.
The following figure illustrates the bus that gets
built when we execute the expression aa | bb
for two 4-gate buses aa and bb.
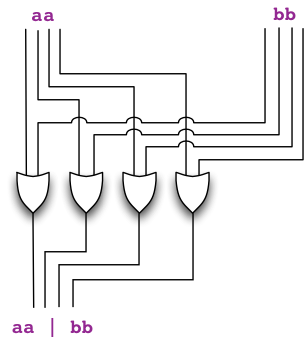
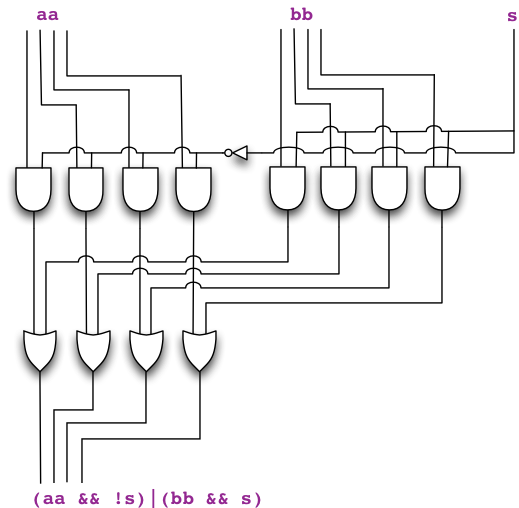
Combining the bus-level operators, we observe that executing
(aa && !s)|(bb && s) indeed constructs the desired selector:
Convention on indexing the bits in a bus
When drawing circuits, it is customary to index the bits in a bus from right to left. That is, the bit with index 0 is the rightmost bit in a bus, and the indices increase from right to left, from the least significant bit to the most significant bit.
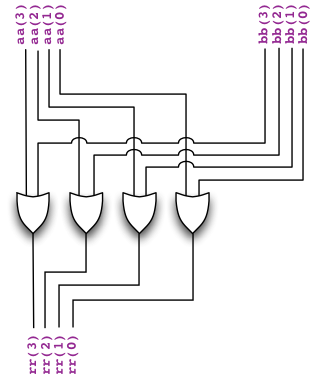
This convention makes it easy to work with buses that carry binary integers, because the integer is displayed on the bus directly in its customary binary form, with the most significant binary digit (bit) on the left, and the least significant binary digit on the right. (Recall our discussion of the positional number system on Round 2: Bits and data.)
Functional design – encapsulating code that builds subcircuits
To arrive at more intricate circuit designs, it is useful to encapsulate circuit-building code into procedures that hide the implementation and enable us to build larger circuits out of smaller component circuits. For example, our two-bus selector can be encapsulated as:
def buildTwoBusSelector(aa: Bus, bb: Bus, s: Gate) =
(aa && !s)|(bb && s)
Here is a builder that reverses the order of bits in a bus:
def buildReverser(aa: Bus) =
aa.reverse
Observe that a reverser actually builds no gates, but rather it simply reverses the order of bits in a bus. We display a reverser for word length 8 below:
Here is a builder that shifts in k zero bits from the
right, and drops k bits out from the left:
def buildLeftShift(aa: Bus, k: Int) =
Bus.falses(k) ++ aa.dropRight(k)
We display a left shift for k = 3 and word length 8 below:
Of course the power of such an approach is revealed when we start
combining builders to yield more complex builders.
Here is a builder for a circuit that outputs either its input aa,
or aa reversed, depending on the value of a control
input s:
def buildIdentityOrReverse(aa: Bus, s: Gate) =
buildTwoBusSelector(aa, buildReverser(aa), s)
Observe how all the attention that we have put into making our tools convenient to use is now starting to pay off.
Here is a shifter that shifts to the left by 1 or 3, depending on
the control input s:
def buildLeftShift1Or3(aa: Bus, s: Gate) =
buildTwoBusSelector(buildLeftShift(aa,1),
buildLeftShift(aa,3),
s)
What about selecting among more than two possibilities?
Here is a builder for a selector (or multiplexer) that
takes a sequence of input buses and a sequence (bus) of
selector bits, and outputs the bus that corresponds to the most
significant selector bit that is set to true, or an
all-false bus if all selector bits are false:
def buildBusSelector(buses: Seq[Bus], selectors: Bus) =
var rr = Bus.falses(buses(0).length)
for i <- 0 until buses.length do
val bb = buses(i)
val s = selectors(i)
rr = buildTwoBusSelector(rr,bb,s)
end for
rr
end buildBusSelector
Here is the same builder but written in a different style that makes
use of the foldLeft operation and a case-expression
to match the components of a tuple:
def buildBusSelector(buses: Seq[Bus], selectors: Bus) =
(buses zip selectors).foldLeft(Bus.falses(buses(0).length)){
case (rr,(bb,s)) => buildTwoBusSelector(rr,bb,s)
}
end buildBusSelector
Let us now combine our tools for a bit of play.
Here is a design for Toggler that shifts the 16-bit input
by any amount of your choosing between 0 and 15 bits to the left:
val n = 16
val input = Bus.inputs(n)
val amount_select = Bus.inputs(n)
val shifts = (0 until n).map(k => buildLeftShift(input, k))
val output = buildBusSelector(shifts, amount_select)
val t = new Toggler()
// reversion will display least significant bit on the right
t.watch("input", input.reverse)
t.watch("amount_select", amount_select.reverse)
t.watch("output", output.reverse)
t.go()
All right, that was fun. But suppose we wanted to give the selection as a binary input? That is, \(b\) bits suffice to select among \(2^{b}\) choices.
Here is a builder for a binary decoder circuit that
takes an integer \(j = 0, 1, \ldots, 2^{b} - 1\)
as a \(b\)-bit bus of input and gives a
\(2^{b}\)-bit bus of output such that on input
\(j\) exactly the output with index \(j\) is true.
def buildDecoder(aa: Bus) =
aa.foldLeft(Bus(Gate.True))((d,a) => (d && !a)++(d && a))
To observe a binary decoder in operation with Toggler, copy and paste
the following code to the console, toggle in any 4-bit binary number
via the inputs, and witness exactly the output indexed by that number
become true among the 16-bit output:
val amount_bits = 4
val input = Bus.inputs(amount_bits)
val output = buildDecoder(input)
val t = new Toggler()
// reversion will display least significant bit on the right
t.watch("input", input.reverse)
t.watch("output", output.reverse)
t.go()
Here is the previous shifter code, but now using a binary decoder so that the shift amount can be given in binary using 4 bits:
val n = 16
val amount_bits = 4 // the base-2 log of n
val input = Bus.inputs(n)
val amount = Bus.inputs(amount_bits)
val shifts = (0 until n).map(k => buildLeftShift(input, k))
val output = buildBusSelector(shifts, buildDecoder(amount))
val t = new Toggler()
// reversion will display least significant bit on the right
t.watch("input", input.reverse)
t.watch("amount", amount.reverse)
t.watch("output", output.reverse)
t.go()
Remark. At this point we should observe and recognize the fruits of our efforts at making our tools convenient. With a few lines of code, we can build and play with intricate circuit designs that accept buses of data input and control input. Think about how many lines of code it would require to build these circuits out of individual gates if we had not paid attention to developing our tools to match the increased complexity.
With our tools sharpened to deal with bus-level designs, we are ready now ready to meet our goal for this round.